ИЗМЕРЕНИЕ УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯ С ПОМОЩЬЮ МАТЕМАТИЧЕСКОГО МАЯТНИКА

Колебаниями называются процессы движения или изменения состояния в той или иной степени повторяющиеся во времени.

В зависимости от физической природы колебательного процесса различают механические, электромагнитные колебания и их комбинации. Свободными являются колебания, которые происходят в отсутствие переменных внешних воздействий и возникают вследствие какого-либо начального отклонения системы из положения равновесия, а затем предоставленной самой себе. Колебания являются периодическими, если значения всех физических величин, характеризующих колебательную систему и изменяющихся при ее колебаниях, повторяются через равные промежутки времени.

Среди разнообразных колебаний, встречающихся в природе, большую роль играют гармонические колебания. Эти колебания представляют собой процесс, в котором изменение какой-либо физической величины происходит по закону синуса или косинуса.

Периодом колебаний Т называется время, за которое совершается одно полное колебание.

Частотой колебаний называется величина 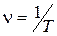, равная числу полных колебаний, совершающихся за единицу времени. Циклической (круговой) частотой колебаний называется величина w, равная .

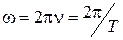Для определения положения тела (материальной точки) в каждый момент времени при гармонических колебаниях вводят понятие смещения, которое обычно обозначают буквой x=x(t). Пусть смещение точки меняется по закону синуса

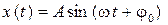. (1.1)

Здесь величина 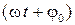называется фазой колебаний, а j₀ – начальной фазой при t=0.

Максимальное отклонение точки от положения равновесия называется амплитудой колебаний и обозначается А.

Зная положение точки в каждый момент времени, определим мгновенную скорость ее движения как производную первого порядка от x(t) по времени

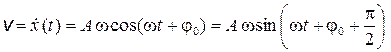. (1.2)

Как видно из формулы (1.2), скорость точки изменяется по тому же закону, что и смещение, однако она сдвинута по фазе на 90°. Амплитуда скорости равна Аw.

Скорость колеблющейся материальной точки максимальна, когда она проходит через положение равновесия. В точках поворота, соответствующих максимальному смещению, скорость точки обращается в нуль. В течение первой четверти цикла, после прохождения положения равновесия в положительном направлении оси скорость положительна. После поворота скорость становится отрицательной и остается такой в течение следующей половины цикла.

Ускорение точки, совершающей гармонические колебания, определяется как производная первого порядка от скорости по времени или как производная второго порядка от смещения

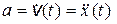. (1.3)

Вычислим производные в (1.3) и получим формулу

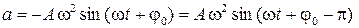. (1.4)

Из (1.4) видно, что амплитуда ускорения определяется величиной Аw². По фазе ускорение отстает от смещения на 180° или, как говорят, ускорение изменяется в противофазе со смещением.

Учитывая (1.1) и (1.3), перепишем выражение (1.4) следующим образом:

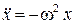, (1.5)

из которого получаем уравнение движения точки при гармонических колебаниях

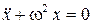. (1.6)

Таким образом, точка совершает гармонические колебания тогда и только тогда, когда ее смещение x(t) удовлетворяет уравнению (1.6), которое называется дифференциальным уравнением гармонических колебаний.

Сила, действующая на материальную точку, равна 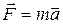. Согласно (1.5), ее проекция на ось OX запишется выражением 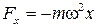, где m – масса материальной точки. Следовательно, сила 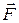пропорциональна смещению точки из положения равновесия и направлена в противоположную сторону. Такая зависимость от смещения характерна для упругой силы. Поэтому силы иной физической природы, удовлетворяющие тому же виду зависимости, называются квазиупругими.

В настоящей работе исследуются свободные колебания математического маятника. Колебания, которые совершает система около положения устойчивого равновесия после того, как она была выведена из этого состояния, называются собственными или свободными колебаниями.

Математическим маятником называется колебательная система, состоящая из тела малых размеров, подвешенного к неподвижной точке на невесомой нерастяжимой длинной нити, такой, что размерами тела, по сравнению с ее длиной, можно пренебречь.

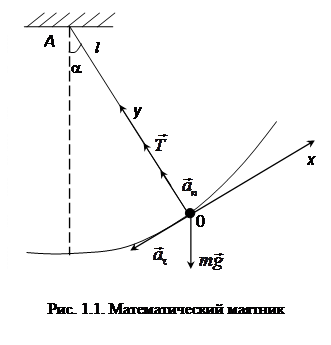
Близким к математическому маятнику можно считать тяжелый шарик, масса которого m, подвешенный на длинной нити l (рис. 1.1). Если шарик отклонить от положения равновесия и отпустить, то математический маятник начнет совершать колебательные движения. При этом на шарик действуют две силы: сила тяжести 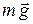и сила натяжения нити .

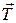Под действием этих сил он движется по дуге окружности, радиус которой равен длине нити l. Это движение неравномерное, так как вектор скорости шарика изменяется не только по направлению, но и по модулю. Ускорение 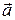, с которым движется шарик в рассматриваемой момент времени в точке О, определяется геометрической суммой нормального ускорения 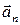и тангенциального 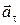: 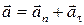. На основании второго закона Ньютона запишем уравнение движения шарика в векторной форме

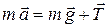. (1.7)

Выберем плоскую систему координат XOY. Направим координатную ось OY из точки О к центру окружности (к точке А, в которой закреплен конец нити), а ось OX – по касательной, приведенной к траектории в точке О. Найдем проекции сил на ось OX и на основании (1.7) запишем уравнение

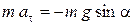, (1.8)

в котором a_t – проекция ускорения 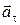на ось OX. Эта проекция определяет скорость измерения модуля скорости шарика 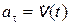. Учитывая (1.3), перепишем уравнение (1.8) в следующем виде:

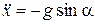. (1.9)

Поскольку в работе рассматриваются гармонические колебания математического маятника, для этого необходимо, чтобы угол максимального отклонения нити от положения равновесия был достаточно малым: угол a_max не должен превышать 10°. При выполнении этого условия можно считать, что 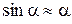, и длина дуги при отклонении маятника на угол a равна 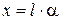. В таком приближении уравнение (1.9) имеет вид

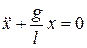. (1.10)

Сравнивая последнее уравнение с (1.6), получаем, что частота гармонических колебаний математического маятника определяется формулой 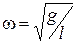, где l – длина математического маятника. Следовательно, для малых углов отклонения период колебаний математического маятника равен

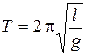. (1.11)

Как видно из (1.11), период колебания маятника не зависит от его массы, а определяется только длиной нити и ускорением свободного падения.

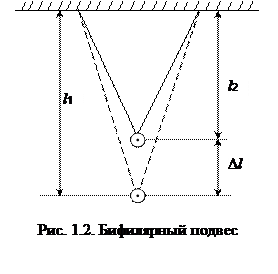
В лабораторной работе в качестве математического маятника используется математический шар, подвешенный на бифилярном подвесе, который совершает колебания строго в одной плоскости (рис. 1.2.)

Рабочая формула для определения ускорения свободного падения получается из (1.11) после несложных преобразований

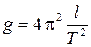. (1.12)

По результатам измерений периода колебаний Т математического маятника и известной длине l можно определить значение ускорения свободного падения g.

Таким образом, в лабораторной работе по формуле (1.12) экспериментально определяется ускорение свободного падения при условии, что бифилярный подвес можно считать математическим маятником.