Центральний не пружний удар двох куль.

При цьому ударі тіла деформуються в точці дотику і потім рухаються з однаковою швидкістю U. Рівняння збереження імпульсу має вигляд

,

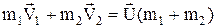і звідси

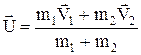. (9)

Робота А, витрачена на деформацію, дорівнює різниці енергій шарів до удару і після удару

,

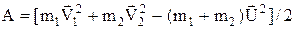і після підстановки значення 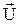з (9) одержимо

.

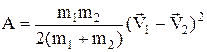2.10.3. Частково пружний удар, коефіцієнт відновлення.

При частково пружному ударі не повністю відновлюється відносна швидкість системи. Можна покласти, що

,

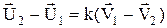де 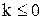¾ коефіцієнт відновлення швидкості. З рівняння збереження імпульсу тепер можна знайти швидкості тіл після удару

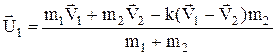, (10)

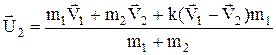. (11)

Рівняння збереження енергії тепер запишеться як

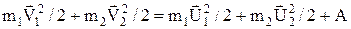. (12)

Підставляючи (10-11) у (12) одержимо величину роботи А на не пружну деформацію тіл

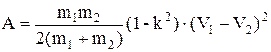. (13)

Робота А чисельно дорівнює втраті тілами кінетичної енергії.

Зауважимо, що при k=1 удар буде абсолютно пружним, при k=0 ¾ не пружним і при 0£ k £1 ¾ частково пружним.

2.11. Принцип відносності Галілея

2.11.1. Механічний принцип відносності Галілеяполягає у тому, що усі механічні явища в різних інерційних системах протікають за однаковими для цих явищ законами за змістом і формою.

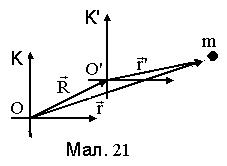
Перетворення координат Галілея: час у різних інерційних системах протікає однаково t=t', а координати при переході з нерухомої системи відліку до рухомої (див. мал. 21) перетворюються лінійно:

,

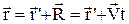де 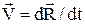швидкість рухомої системи відносно нерухомої.

З цього виразу можна одержати рівняння перетворення швидкостей

.

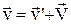В цьому виразі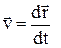¾абсолютнашвидкість, тобто швидкість тіла в нерухомій системі відліку, 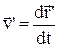¾швидкість тіла в рухомій системі відліку, яку називають відносною. Такі ж вирази можна одержати і для прискорень, .

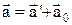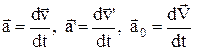2.11.2. Рівняння другого закону Ньютона в нерухомій системі відліку має вигляд 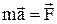m, в рухомій ¾ 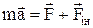, де 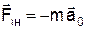¾ сила інерції.

У випадку, коли система K' інерційна, тоб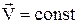то , то 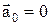, 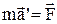і рівняння другого закону Ньютона зберігають свій вигляд як у нерухомій так і у рухомій інерційній системі відліку. Це і пояснює принцип відносності Галілея.

2.12.Динаміка обертового руху