Задание 1. Определение ускорения свободного падения с помощью математического маятника.
1. Установив любое значение длины математического маятника l (расстояние от точки подвеса – до черты, нанесенной на шарик) в интервале от 35 до 40 см, измерьте период его колебаний Т. Затем, увеличив l на несколько сантиметров, опять измерьте Т и т. д. Шаг измерения l выберите таким образом, чтобы измерения Т были проведены не менее чем при 6 ÷ 8 значениях l. В результате получится набор значений периодов колебаний Ti, соответствующих длинам маятника li, где i – номер опыта. При каждом значении l измерения периода проводите 3 раза и усредняйте полученные значения.
2. Данные занесите в таблицу:
Таблица
| № п/п |  , см , см
| Т1, сек | Т2, сек | Т3, сек | 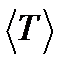 , сек , сек
| 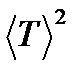 , сек , сек
|
3. Постройте график зависимости 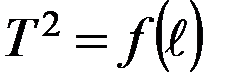
По данным из таблицы отложите по оси абсцисс значения 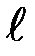 , а по оси ординат – значения переменной у = Т2 и нанесите на график экспериментальные точки. Проведите через них наилучшую прямую (т. е. такую, чтобы отклонение каждой экспериментальной точки от данной прямой было примерно одинаковым). Проведите эту прямую вначале на глаз, а затем используя метод наименьших квадратов.
, а по оси ординат – значения переменной у = Т2 и нанесите на график экспериментальные точки. Проведите через них наилучшую прямую (т. е. такую, чтобы отклонение каждой экспериментальной точки от данной прямой было примерно одинаковым). Проведите эту прямую вначале на глаз, а затем используя метод наименьших квадратов.
Т2, с С
Е Д
0 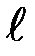 , см
, см
4. Значения Т и 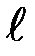 для математического маятника связаны между собой зависимостью (2), поэтому
для математического маятника связаны между собой зависимостью (2), поэтому
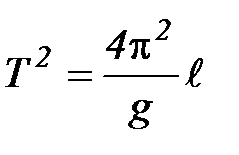 или Y = Al (3)
или Y = Al (3)
где 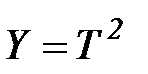 ,
, 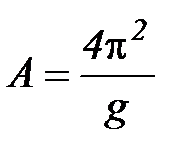 . Следовательно, согласно теории прямая на координатной плоскости (Y, X) должна проходить через начало координат. Опыт, однако, показывает, что наилучшая прямая не проходит через начало координат (подумайте о возможных причинах этого!). Поэтому по рисунку определяют угловой коэффициент прямой как отношение длин отрезков СД и ЕД:
. Следовательно, согласно теории прямая на координатной плоскости (Y, X) должна проходить через начало координат. Опыт, однако, показывает, что наилучшая прямая не проходит через начало координат (подумайте о возможных причинах этого!). Поэтому по рисунку определяют угловой коэффициент прямой как отношение длин отрезков СД и ЕД:
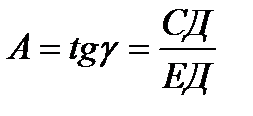 . Тогда
. Тогда
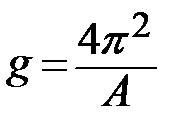 (4)
(4)
Определите ускорение свободного падения gпо формуле (4).
5. Рассчитайте погрешность измерения ускорения свободного падения gпо формуле:
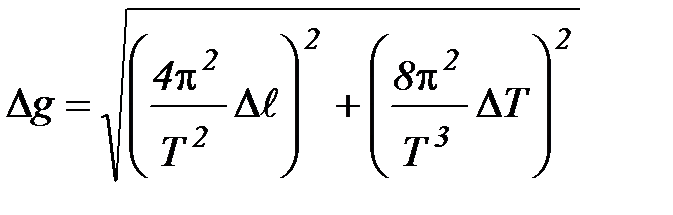 ,
,
где 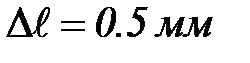 ;
; 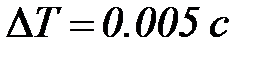 .
.
Дата добавления: 2015-11-18; просмотров: 1852;
