ИЗУЧЕНИЕ НЕУПРУГОГО УДАРА
1. Цель работы:изучение методики применения законов сохранения для неупругого удара шаров и методики обработки стробоскопических фотографий процесса столкновения.
2. Приборы и принадлежности:набор стробоскопических фотографий; циркуль; линейка.
Методика и порядок выполнения работы.
Ударом называется кратковременное взаимодействие тел, двигающихся до этого с различными скоростями, при их соприкосновении, в результате которого резко изменяется состояние их движения. При этом предполагается, что до и после удара тела не взаимодействуют. При ударе тела деформируются, и в результате возникают силы взаимодействия, препятствующие деформациям, и направленные противоположно относительным скоростям соударяющихся тел. За счет работы этих сил происходит перераспределение энергии между соударяющимися телами.
Различают два предельных типа удара: абсолютно неупругий и абсолютно упругий. Оба этих типа являются идеализированными схемами реальных явлений удара.
Прямая, совпадающая с нормалью к поверхностям соударяющихся тел в точке соприкосновения, то есть к общей касательной плоскости называется линией удара (рисунок 1). Удар называется центральным, если линия удара проходит через центры масс С1 и С2 тел (на рисунке 1 удар не является центральным). Удар двух однородных шаров всегда будет центральным.
| линия удара |
| касательная |
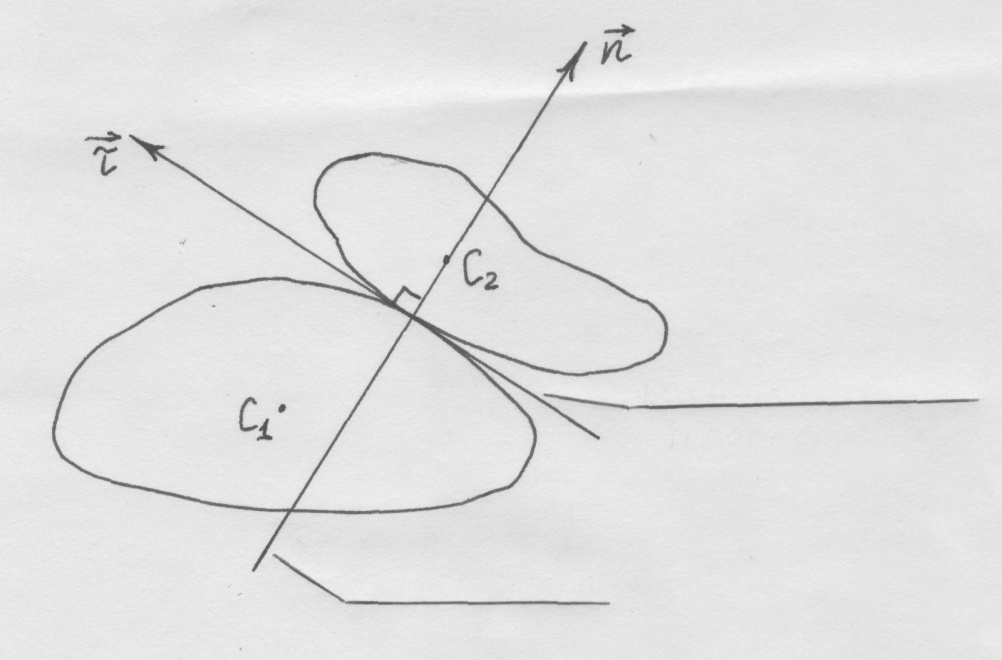
Рисунок 1 – Линия удара
При прямом ударе оба соударяющихся тела до удара двигаются вдоль линии удара; в противном случае удар называется косым. Рассмотрим косой удар двух шаров 1 и 2 с массами m1 и m2 соответственно (рисунок 2). Пусть 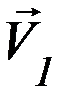 ,
, 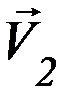 – скорости шаров до
– скорости шаров до
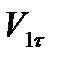
|
| С1 |
| С2 |
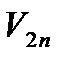
|
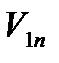
|
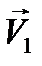
|
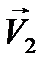
|
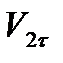
|
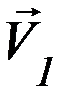 ,
, 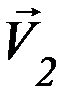 на линию удара назовем нормальными составляющими и обозначим V1n, V2n, а на перпендикулярное к линии удара направление касательной к шарам в точке их соприкосновения – тангенциальными составляющими V1τ, V2τ.
на линию удара назовем нормальными составляющими и обозначим V1n, V2n, а на перпендикулярное к линии удара направление касательной к шарам в точке их соприкосновения – тангенциальными составляющими V1τ, V2τ.
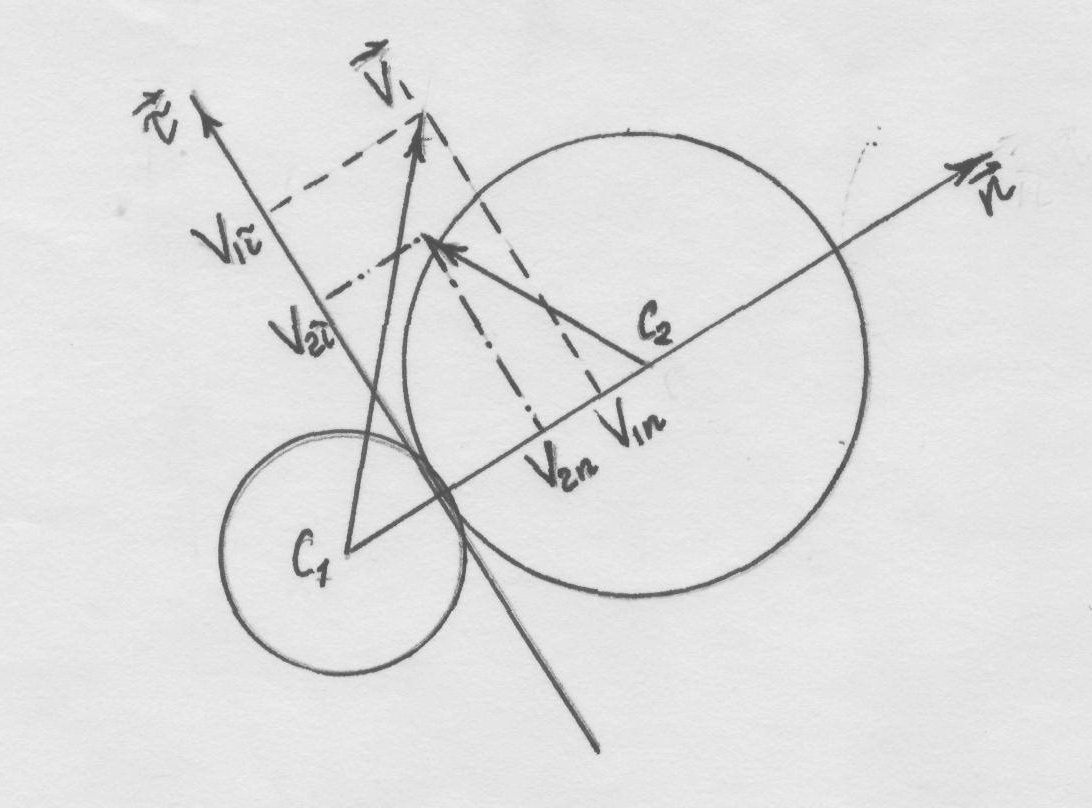
Рисунок 2 – Косой удар двух шаров
Косой удар двух шаров называется абсолютно неупругим, если после удара нормальные составляющие скоростей оказываются одинаковыми (скорости после удара и их проекции в дальнейшем обозначаются так: 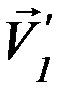 ,
, 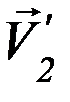 ,
, 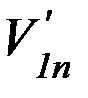 ,
, 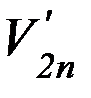 ,
, 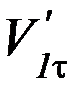 ,
, 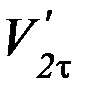 . После абсолютно неупругого удара тела остаются в деформированном состоянии. В частности, если удар прямой, то до удара:
. После абсолютно неупругого удара тела остаются в деформированном состоянии. В частности, если удар прямой, то до удара:
V1τ = V2τ = 0
и после удара оба тела движутся вместе как единое целое. Рассмотрим процесс соударения. Нормальные составляющие скоростей тел до удара V1n, V2n могут быть изменены при ударе только параллельно им направленными силами взаимодействия, возникающими при деформации тел. Для того, чтобы после удара нормальные составляющие скоростей тел 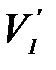 и
и 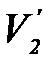 оказались одинаковыми, необходимо, чтобы силы, возникающие в процессе взаимодействия, зависели не от величины деформаций, а от их скорости. Силы эти должны быть значительными даже при небольших, но быстро меняющихся деформациях. Если же деформации не изменяются со временем, то даже если они большие, силы должны обращаться в нуль.
оказались одинаковыми, необходимо, чтобы силы, возникающие в процессе взаимодействия, зависели не от величины деформаций, а от их скорости. Силы эти должны быть значительными даже при небольших, но быстро меняющихся деформациях. Если же деформации не изменяются со временем, то даже если они большие, силы должны обращаться в нуль.
Существование таких сил подтверждается опытными фактами, показывающими, что пластичные тела очень трудно деформировать кратковременным воздействием (ударом), но они очень легко деформируются при длительном воздействии даже малых сил. Поскольку нормальные составляющие V1n, V2n скоростей тел до удара различны, в начале процесса соударения деформации обоих тел будут изменяться быстро, и при этом возникнут значительные силы взаимодействия, препятствующие деформациям. Под действием этих сил нормальные составляющие скоростей изменяются до тех пор, пока не станут равными, т. е. после удара 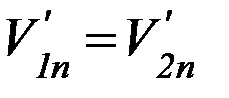 . К этому моменту времени деформация обоих тел достигают максимальной величины, но их изменения прекращаются. Одновременно обращаются в нуль и составляющие сил взаимодействия вдоль линии удара, так что дальнейшее изменение нормальных составляющих скоростей прекращается. Пусть система шаров замкнута, т. е. шары не взаимодействуют с окружающими телами, а только между собой. Тогда для процесса взаимодействия шаров выполняется закон сохранения импульса в векторной форме:
. К этому моменту времени деформация обоих тел достигают максимальной величины, но их изменения прекращаются. Одновременно обращаются в нуль и составляющие сил взаимодействия вдоль линии удара, так что дальнейшее изменение нормальных составляющих скоростей прекращается. Пусть система шаров замкнута, т. е. шары не взаимодействуют с окружающими телами, а только между собой. Тогда для процесса взаимодействия шаров выполняется закон сохранения импульса в векторной форме:
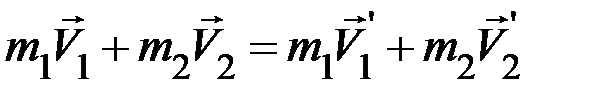 , (1)
, (1)
где 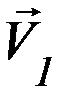 ,
, 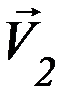 – векторы скоростей шаров после удара.
– векторы скоростей шаров после удара.
Спроектируем уравнение (1) на линию удара и на касательную к шарам в точке их соприкосновения. Получим
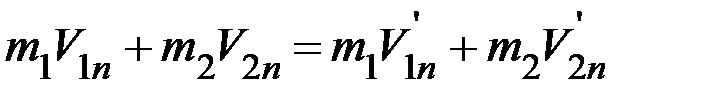 (2)
(2)
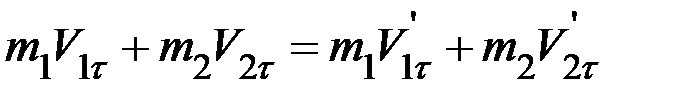
Согласно определению абсолютно неупругого удара 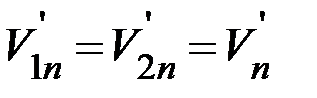 .
.
Поэтому (2) можно переписать в виде:
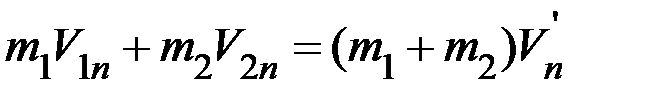 (3)
(3)
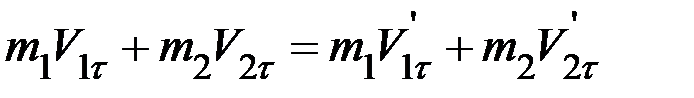
Если известны m1, m2 и V1n, V2n то из первого уравнения системы (3) можно найти нормальную составляющую скоростей шаров после удара 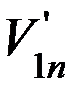 :
:
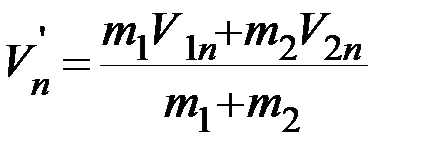 (4)
(4)
Что касается тангенциальных составляющих 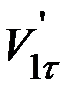 и
и 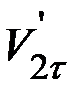 после удара, то одного второго уравнения системы (3) для их определения недостаточно, даже если известны
после удара, то одного второго уравнения системы (3) для их определения недостаточно, даже если известны 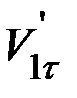 и
и 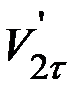 до удара. Изменить эти составляющие в процессе удара могут лишь параллельно им направленные силы – силы трения. Не зная времени взаимодействия и не делая никаких предположений о характере сил трения, определить
до удара. Изменить эти составляющие в процессе удара могут лишь параллельно им направленные силы – силы трения. Не зная времени взаимодействия и не делая никаких предположений о характере сил трения, определить 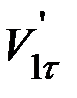 и
и 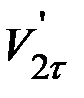 невозможно. В частности, нельзя однозначно утверждать, что
невозможно. В частности, нельзя однозначно утверждать, что 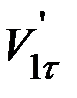 =
= 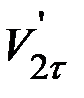 . Силы трения, возникающие между шарами при ударе, вызывают вращение шаров после удара, так что процесс удара становится очень сложным. В некоторых случаях, однако, силами трения при ударе можно пренебречь. В этом случае, согласно вышеуказанному, тангенциальные составляющие скоростей шаров после удара равны соответствующим тангенциальным составляющим скоростей до удара:
. Силы трения, возникающие между шарами при ударе, вызывают вращение шаров после удара, так что процесс удара становится очень сложным. В некоторых случаях, однако, силами трения при ударе можно пренебречь. В этом случае, согласно вышеуказанному, тангенциальные составляющие скоростей шаров после удара равны соответствующим тангенциальным составляющим скоростей до удара:
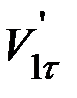 =
= 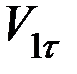 ,
, 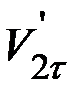 =
= 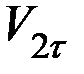 (5)
(5)
Шары после удара в этом случае не вращаются. Из системы уравнений (1-3) можно найти отношение масс шаров, если известны кинематические характеристики их движения до и после удара:
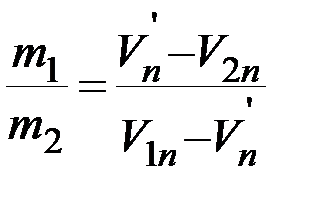 (6)
(6)
Если известно движение первого шара до и после удара, а движение второго шара после удара нужно найти, то, решая систему (1-3), находим:
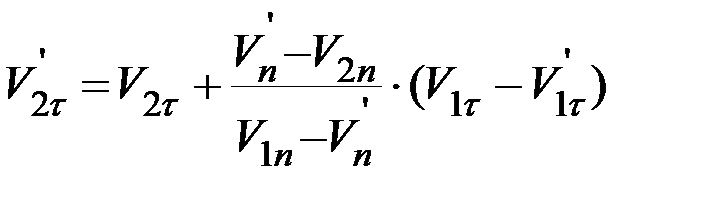 (7)
(7)
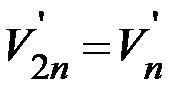 ,
,
так что вектор скорости второго шара после удара находится однозначно, если его движение до удара известно. При абсолютно неупругом ударе не выполняется закон сохранения механической энергии. Это объясняется тем, что силы взаимодействия между шарами, зависящие от скоростей деформаций, не являются консервативными, а диссипативными. То же относится, конечно, и к силам трения между шарами, если они есть. Изменение механической энергии шаров в процессе столкновения в том случае, когда силы трения отсутствуют (так что вращение шаров после удара также отсутствуют) дается выражением
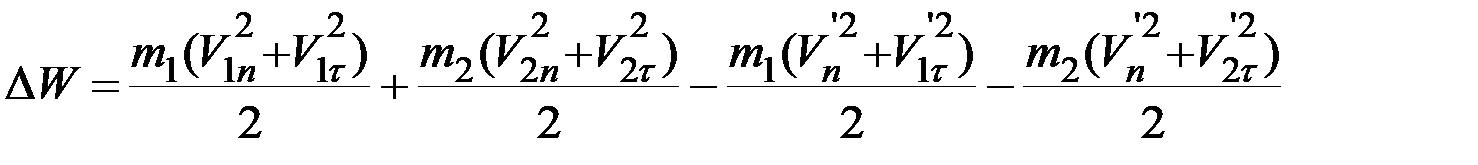 (8)
(8)
Процесс соударения шаров удобно исследовать с помощью стробоскопических фотографий. Стробоскопические фотографии получаются путем открывания затвора фотоаппарата через строго фиксированные промежутки времени, величина которых может регулироваться. Для того, чтобы за время, когда затвор открыт, тела не могли заметно сместиться, это время должно быть достаточно малым, поэтому для получения на пленке достаточно яркого изображения используются мощные, чаще всего импульсные, работающие синхронно с затвором, осветители. На стробоскопических фотографиях получаются положения тел через строго фиксированный промежуток времени τ, называемый периодом стробоскопирования. Выбирая τ малым, можно с высокой степенью точности исследовать форму траектории тела, найти его скорость и ускорение. Особенно просто находятся кинематические характеристики движения, если траектория – прямая линия. На рисунке 3 представлен пример стробоскопической фотографии движущегося в направлении, указанном стрелкой шара.
| L3 |
| |
| L1 |
| L2 |
| t=0 |
| t=τ |
| t=2τ |
Рисунок 3 – Стробоскопическая фотография шара
Если заранее из каких-либо соображений известно, что движение равномерное, то скорость шарика может быть найдена из очевидного соотношения:
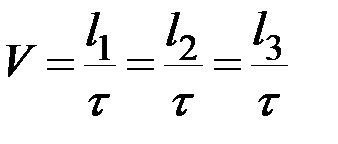 , (9)
, (9)
где τ – период стробоскопирования. (Хотя шарик, судя по фотографии, за равные промежутки времени проходит равные пути l1 = l2 = …, это не дает возможности утверждать, что движение равномерное: оно может быть и неравномерным (почему?) – для равномерности движения необходимо, чтобы за любые равные промежутки времени тело проходило равные пути). Направление вектора скорости устанавливается в данном случае очевидным образом. Если имеется стробоскопическая фотография двух движущихся тел, например, шариков, то по ней можно установить, сталкиваются ли шарики, если сталкиваются, то каково расположение их в момент столкновения, в какой момент времени произойдет столкновение и т. д. Рассмотрим пример. На рисунке 4 изображены два шара радиусами R1 и R2, движущиеся по пересекающимся прямым. Буквами А, В помечены начальные расположения центров шаров; 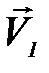 ,
, 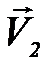 – их скорости. Для выяснения вопроса, столкнутся ли шары, удобно перейти в систему отсчета, в которой, например, шар 1 покоится. В этой системе отсчета шар 2 движется со скоростью
– их скорости. Для выяснения вопроса, столкнутся ли шары, удобно перейти в систему отсчета, в которой, например, шар 1 покоится. В этой системе отсчета шар 2 движется со скоростью 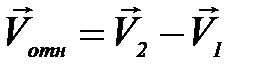 относительно первого шара. При движении со скоростью
относительно первого шара. При движении со скоростью 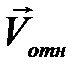 в системе отсчета, в которой первый шар покоится, шар 2 описывает цилиндр С, образующие которого параллельны вектору
в системе отсчета, в которой первый шар покоится, шар 2 описывает цилиндр С, образующие которого параллельны вектору 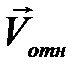 . Если шар 1 пересекает поверхность этого цилиндра – столкновение происходит; в противном случае – нет. Расстояние между центром шара 1 и линией BB″ движения второго шара, обозначенное на рисунке через P, называется прицельным параметром. Очевидно, столкновение происходит, если P ≤ R1 + R2. На рисунок 4 столкновение происходит, причем в момент соприкосновения центр шара 2 находится в точке B″, отстоящей от
. Если шар 1 пересекает поверхность этого цилиндра – столкновение происходит; в противном случае – нет. Расстояние между центром шара 1 и линией BB″ движения второго шара, обозначенное на рисунке через P, называется прицельным параметром. Очевидно, столкновение происходит, если P ≤ R1 + R2. На рисунок 4 столкновение происходит, причем в момент соприкосновения центр шара 2 находится в точке B″, отстоящей от
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| Р |
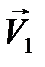
|
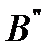
|
| А1 |
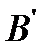
|
| В |
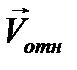
|
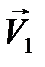
|
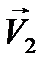
|
| А |
| линия удара |
| С |
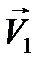
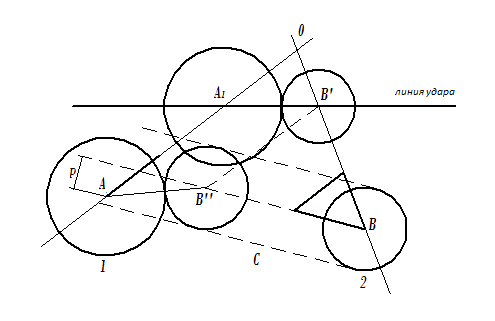
Рисунок 4 – Движение двух шаров А и В
Выполнив это построение и измеряя затем расстояние |B″| и 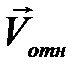 по чертежу, нетрудно определить и момент соударения:
по чертежу, нетрудно определить и момент соударения:
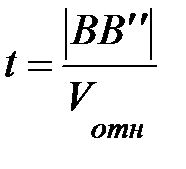 (10)
(10)
Переход в неподвижную систему отсчета осуществляется следующим образом: в неподвижной системе отсчета центр шара 2 движется вдоль линии 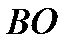 , поэтому, снося точку B″ на линию ВО, получаем положение B´ центра шара 2 в момент соприкосновения в неподвижной системе отсчета. Проводя A´B´||AB″, находим и положение центра шара 1 в момент удара (А´). Момент соударения теперь можно определить таким образом:
, поэтому, снося точку B″ на линию ВО, получаем положение B´ центра шара 2 в момент соприкосновения в неподвижной системе отсчета. Проводя A´B´||AB″, находим и положение центра шара 1 в момент удара (А´). Момент соударения теперь можно определить таким образом:
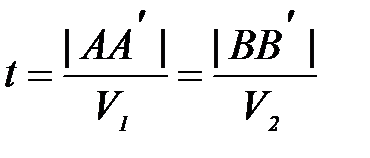 , (11)
, (11)
что позволяет проконтролировать ранее полученный результат в формуле (9). Очевидно, прямая А´B´ является линией удара.
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| Р |
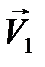
|
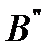
|
| А1 |
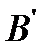
|
| В |
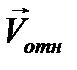
|
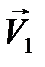
|
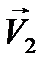
|
| А |
| линия удара |
| С |
Задание 2. На фотографии (рисунок 6) период стробоскопирования τ выбирается аналогично заданию 1. Аналогично же заданию 1 выясните, столкнутся ли шарики. Найдите момент соударения, усредняя результаты, полученные по формулам (1-10) (1-11). Сделайте чертеж и изобразите на нем линию удара шаров.
Задание 3. На фотографии (рисунок 7) период стробоскопирования выбирается аналогично предыдущим заданиям. Найдите скорости шаров до удара V1 и V2 и изобразите их графически в удобном масштабе. Найдите аналогично заданию 2 линию удара и спроектируйте векторы скоростей на линию удара и на направление касательной к шарам в точке их соприкосновения. Найдите аналогично рисунку 2 V1n, V1τ, V2n, V2τ до удара. При этом учтите, что величины V1n, V1τ, V2n, V2τ – величины алгебраические. Так, например, если положительными направлениями на рисунке 2 считать направление вправо и вверх (они помечены стрелками), то V1n > 0, V2n < 0, V1τ > 0, V2τ > 0. Аналогично найти проекции скоростей после удара 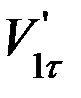 ,
, 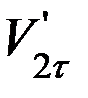 ,
, 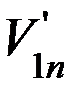 ,
, 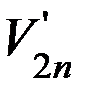 с учетом знаков. Внимание! Все скорости откладывать в одинаковом масштабе.
с учетом знаков. Внимание! Все скорости откладывать в одинаковом масштабе.
Примечание: Деформации шаров в процессе удара были незначительными, поэтому на фотографии они незаметны.
Задание 4. На фотографии (рисунок 8) период стробоскопирования выбирается аналогично предыдущим заданиям, массы шаров m1, m2 – из таблицы (имеет прежний смысл). Найдите скорости шаров до удара V1 и V2, положение шаров в момент соударения и V1n, V2n, V1τ, V2τ. По формуле (4) найдите нормальные составляющие скоростей после удара 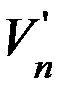 . Тангенциальные составляющие скоростей после удара найдите исходя из предположения, что силы трения отсутствуют (формула (5)). Изобразите на чертеже скорости шаров до и после удара в одинаковом масштабе и изобразите положения центров шаров после удара за промежуток времени, равный утроенному периоду стробоскопирования. Рассчитайте изменение внутренней энергии шаров в процессе удара по формуле (8).
. Тангенциальные составляющие скоростей после удара найдите исходя из предположения, что силы трения отсутствуют (формула (5)). Изобразите на чертеже скорости шаров до и после удара в одинаковом масштабе и изобразите положения центров шаров после удара за промежуток времени, равный утроенному периоду стробоскопирования. Рассчитайте изменение внутренней энергии шаров в процессе удара по формуле (8).
Задание 5. На стробоскопической фотографии (рисунок 9) изображено движение обоих шаров до удара, а после удара - только одного шара. Период стробоскопирования выбирается аналогично предыдущему. По формулам (7) найдите для второго шара 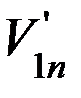 и
и 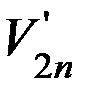 и нарисуйте, как будет двигаться второй шар после удара. Изобразите на чертеже полную стробоскопическую фотографию картины соударения шаров и найдите отношение масс шаров по формуле (5).
и нарисуйте, как будет двигаться второй шар после удара. Изобразите на чертеже полную стробоскопическую фотографию картины соударения шаров и найдите отношение масс шаров по формуле (5).
Примечание: Во всех заданиях допускается приводить численное значение всех скоростей и составляющих в столбце прямо на чертеже. При этом на чертеже должен быть обязательно указан масштаб расстояний (если чертеж уменьшается) и масштаб скоростей. Продумайте методику расчета погрешностей.
Дата добавления: 2015-11-18; просмотров: 1448;
