Задания для самостоятельной работы. 1. Установите нижний кронштейн на расстоянии h1 = 0,15 м от верхнего кронштейна (4)

1. Установите нижний кронштейн на расстоянии h₁ = 0,15 м от верхнего кронштейна (4). Проведите измерения времени движения диска 3-4 раза и найдите среднее время движения t₁.

2. Определите ускорение центра масс диска Максвелла по формуле:

,

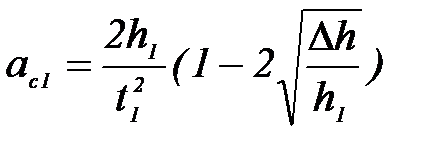где ∆h = 3∙10^{-3 м (Приложение 3).}

3. Повторите вычисление ускорения центра масс при значениях h = 0,15÷0,4 м с шагом 0,05 м и найти среднее значение ускорения (n – количество измерений)

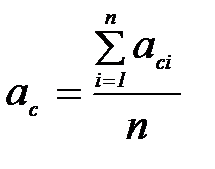
4. Вычислите момент инерции диска Максвелла (J_с) относительно оси, проходящей через центр масс по формуле (Приложение 2):

,

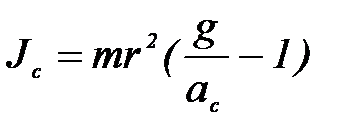где М – масса системы, r – радиус намотки, g = 9,8 м/с² – ускорение свободного падения.

5. Вычислите согласно Приложению 3 величины

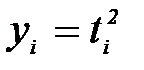
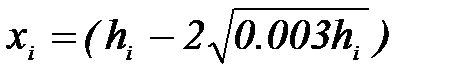
На координатную плоскость (Х, У) нанести экспериментальные точки. Согласно теории зависимость между величинами Х и У линейная: У = АХ. Проведите через начало координат и экспериментальные точки наилучшую с Вашей точки зрения прямую и найдите её угловой коэффициент А.

6. По формуле:

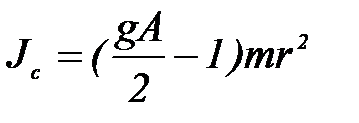
Опять найдите момент инерции J_c и сравните с результатами п. 4.

7. Согласно методу наименьших квадратов (Приложение 3) значение А находится по формуле:

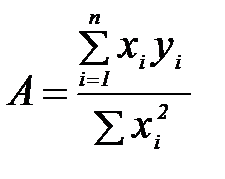
Найдите это значение A и значение I_c и сравните с найденными ранее значениями.

8. Рассчитайте погрешность определения I_c по формуле:

,

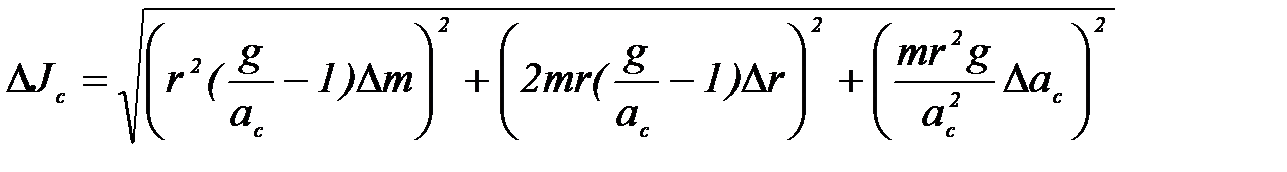учитывая для a_c лишь погрешности разброса. Погрешности массы и радиуса намотки принять равными: ∆m = 1 г; ∆r = 1 мм.

9. Вычислите теоретическое значение момента инерции системы по стандартным формулам и указанными на рабочем месте характеристикам системы и сравните с найденными экспериментальными значениями.