Приложение. Теория малых колебаний физического маятника.
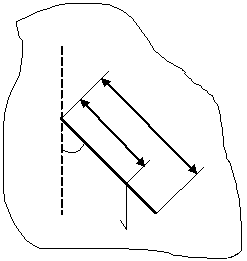
| mg |
| φ |
| o |
| c |
| O’ |
| Рисунок 3 3. Приведенная длина |
Движение маятника описывается основным уравнением динамики вращательного движения вокруг неподвижной оси:
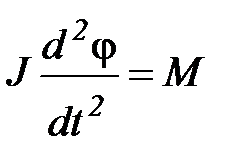 ,
,
где J – момент инерции маятника относительно оси вращения, φ – угол отклонения маятника от положения равновесия, М – суммарный момент внешних сил, действующих на маятник относительно оси вращения.
В экспериментальных установках обычно моменты силы трения в оси и силы сопротивления воздуха пренебрежимо малы. Поэтому Мс = – mgd sinφ, где
d = │ОС│ – расстояние от оси качания до центра масс, m – масса маятника,
g – ускорение свободного падения, а знак " – " указывает на то, что момент силы тяжести стремится возвратить маятник в положение равновесия. Таким образом, уравнение движения маятника имеет вид:
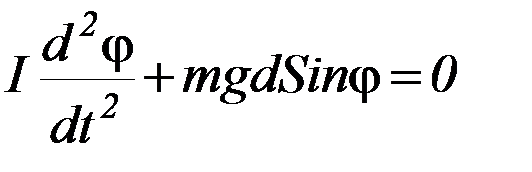 (П-1)
(П-1)
В случае малых отклонений маятника от положения равновесия (т.е. φ << 1) можно положить sin φ ≈ φ. Тогда уравнение (П-1) примет вид:
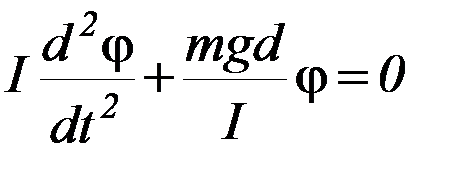 (П-2)
(П-2)
Легко убедиться, что решением этого уравнения является функция
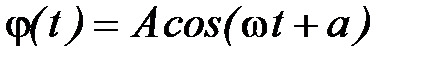
где 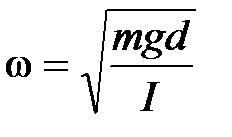 , а А и α – произвольные постоянные, т.е. величина φ(t) совершает гармонические колебания с циклической частотой ω. Амплитуда А и начальная фаза колебаний α зависят от способа возбуждений колебаний, т.е. определяются значениями φ и
, а А и α – произвольные постоянные, т.е. величина φ(t) совершает гармонические колебания с циклической частотой ω. Амплитуда А и начальная фаза колебаний α зависят от способа возбуждений колебаний, т.е. определяются значениями φ и 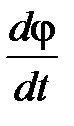 в момент времени t = 0. Частота колебаний ω определяется только параметрами маятника m, J, d.
в момент времени t = 0. Частота колебаний ω определяется только параметрами маятника m, J, d.
Таким образом, при малых углах отклонения от положения равновесия колебания физического маятника являются гармоническими с периодом
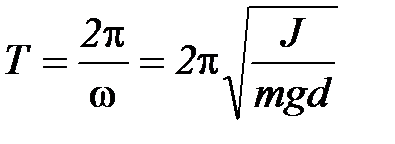 , (П-3)
, (П-3)
причем период колебаний не зависит ни от начальной фазы, ни от амплитуды колебаний, а определяется только параметрами маятника.
Согласно теореме Гюйгенса-Штейнера момент инерции маятника J относительно оси вращения можно представить в виде:
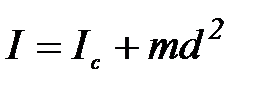 , (П-4)
, (П-4)
где Jc – момент инерции маятника относительно оси, проходящей через его центр масс.
Используя (П-4), формулу (П-3) можно переписать следующим образом:
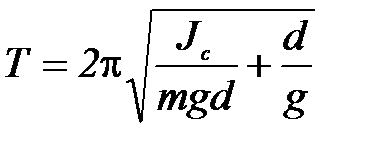 (П-5)
(П-5)
Частным случаем физического маятника является математический маятник. Это идеализированная система, состоящая из невесомой нерастяжимой нити, на которой подвешена масса, сосредоточенная в одной точке – центре масс маятника С. Для математического маятника длиной 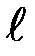 имеем: d =
имеем: d = 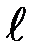 . Jc = 0. Тогда формула (П-5) принимает вид:
. Jc = 0. Тогда формула (П-5) принимает вид:
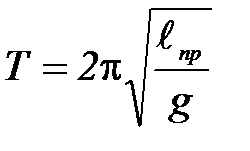 (П-6)
(П-6)
Сравнение формул (П-5) и (П-6) показывает, что период колебаний физического маятника равняется периоду колебаний математического маятника длиной
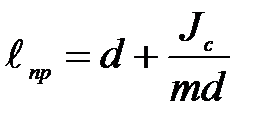 (П-7)
(П-7)
Величину lпр называют приведённой длиной физического маятника. Таким образом, приведенная длина физического маятника – это длина такого математического маятника, период колебаний которого равен периоду колебаний данного физического маятника.
Как следует из (П-7), приведенная длина физического маятника больше, чем расстояние от оси качания до центра масс маятника. Точка О, находящаяся от точки 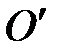 на расстоянии lпр вдоль прямой, соединяющей точку подвеса с центром масс, называется центром качаний. Если маятник подвесить в точке
на расстоянии lпр вдоль прямой, соединяющей точку подвеса с центром масс, называется центром качаний. Если маятник подвесить в точке 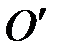 , то период его колебаний будет тот же, что и при подвешивании в точке О. Действительно, при подвешивании маятника в точке
, то период его колебаний будет тот же, что и при подвешивании в точке О. Действительно, при подвешивании маятника в точке 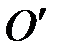 , из (П-5) получаем следующее выражение для периода колебаний:
, из (П-5) получаем следующее выражение для периода колебаний:
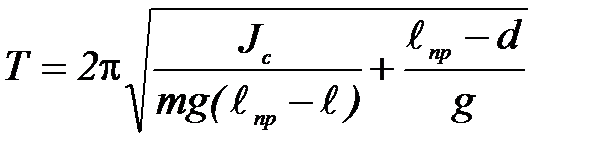 (П-8)
(П-8)
Из (П-7) имеем: 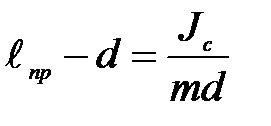
Тогда 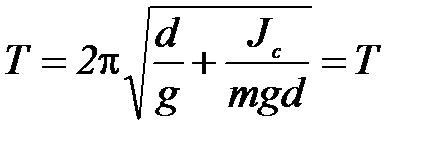
Таким образом, период колебаний физического маятника не изменяется при перемещении оси качаний в центр качаний.
Дата добавления: 2015-11-18; просмотров: 1932;
