Задание 2. Определение ускорения свободного падения с помощью оборотного маятника и момента инерции Jc оборотного маятника
1. Зафиксируйте чечевицы на стержне оборотного маятника таким образом, чтобы одна из них находилась вблизи конца стержня, а другая – вблизи его середины (см. рисунок 2).
| C |
| 1 2 |
| d1d2 |
Рисунок 2 – Оборотный маятник
Одну из опорных призм зафиксируйте вблизи свободного конца стержня, а вторую – между чечевицами, причем опорные проемы должны быть обращены друг к другу.
2. Определите положение центра масс (т. С) оборотного маятника, уравновешивая его на дополнительной опорной призме, расположенной на лабораторном столе. Если оказалось, что центр массы маятника находится между опорными призмами, значит, оборотный маятник собран правильно.
Чтобы точность определения ускорения свободного падения была достаточно высокой, необходимо, чтобы расстояния d1 и d2 от центра масс (т. С) до опорных призм, удовлетворяли условию:
1,5d2 < d1 < 3d2 (5)
Используя нарезки на стержне оборотного маятника, установите опорную призму, находящуюся между чечевицами на расстоянии d2 = 10 ÷ 15 см от центра масс маятника. Вторую опорную призму зафиксируйте на таком расстоянии d1 от центра масс маятника, которое удовлетворяет неравенству (5).
3. Установив маятник на вкладыши верхнего кронштейна опорной призмой, находящейся вблизи свободного конца стержня на расстоянии d1 от центра масс маятника, измерьте период его колебаний Т1. Затем переверните маятник и, установив его на вкладыши верхнего кронштейна опорной призмой, находящейся между чечевицами, измерьте период его колебаний Т2.
4. Используя измеренные значения d1, d2, T1, Т2, решите систему уравнений (6) и (7) и рассчитайте ускорение свободного падения g и момент инерциимаятника Jc относительно оси, проходящей через его центр масс.
Теория даёт следующие уравнения для нахождения периода оборотного маятника:
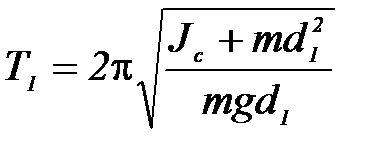 (6)
(6)
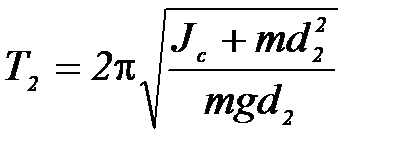 , (7)
, (7)
где m – масса всего маятника; Jc – момент инерции маятника относительно оси, проходящей через т. С (центр масс маятника)
5. Не изменяя положения чечевиц, повторите измерения при других значениях d1, d2 удовлетворяющих условию (5), и результаты Jc и g, полученные в пунктах 4) и 5) усредните.
6. Рассчитайте относительные погрешности определения ускорения свободного падения и момента инерции оборотного маятника ( 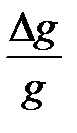 ,
, 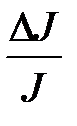 ).
).
В силу сложности математического выражения для определения данной погрешности можно воспользоваться упрощённым вариантом расчёта. Для этого относительные погрешности прямым образом определяемых величин (M, d, T) принять равными: 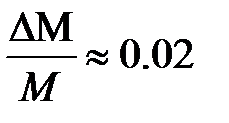 ;
; 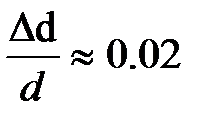 . (В данной работе период рассматриваем как прямым образом измеренную величину). Относительной погрешностью измерения периода в силу малости можно пренебречь. Рассчитайте относительную погрешность определениямомента инерции и коэффициента упругих сил кручения как сумму относительных погрешностей прямым образом определяемых величин.
. (В данной работе период рассматриваем как прямым образом измеренную величину). Относительной погрешностью измерения периода в силу малости можно пренебречь. Рассчитайте относительную погрешность определениямомента инерции и коэффициента упругих сил кручения как сумму относительных погрешностей прямым образом определяемых величин.
Дата добавления: 2015-11-18; просмотров: 1235;
