ИЗУЧЕНИЕ ФИЗИЧЕСКОГО И МАТЕМАТИЧЕСКОГО МАЯТНИКОВ

Цель работы:

– экспериментальная проверка зависимостей между физическими величинами, характеризующими колебания математического и оборотного маятников;

– экспериментальное определение ускорения свободного падения g помощью математического маятника;

– экспериментальное определение ускорения свободного падения с помощью оборотного маятника.

Приборы и принадлежности:

– универсальный маятник FPM-4 с миллисекундомером и счетчиком числа периодов.

Описание установки

Рисунок 1 – Общий вид установки FRM-04

Общий вид универсального маятника FPM-04 представлен на рис. 1.

Основание (1) оснащено регулируемыми ножками (2), которые позволяют произвести горизонтальную установку прибора. В основании закреплена колонка (3), на которой зафиксированы верхний кронштейн (4) и нижний кронштейн (5) с фотоэлектрическим датчиком (6).

После отвинчивания воротка (11) верхний кронштейн (4) можно поворачивать вокруг колонки. Затяжка воротка (11) фиксирует кронштейн в любом произвольно выбранном положении. С одной стороны кронштейна (4) находится математический маятник (7), с другой, на вмонтированных вкладышах - оборотный маятник (8). Оба маятника – математический и оборотный – представляют собой различные реализации физического маятника.

Длина математического маятника может регулироваться при помощи воротка (9) и определяется положением верхнего кронштейна (5) относительно шкалы на колонке (3). При этом маятник должен быть установлен таким образом, чтобы черта на шарике (7) была продолжением черты на корпусе фотоэлектрического датчика (6).

Оборотный маятник (8) выполнен в виде стального стержня, на котором зафиксированы две опорные призмы (12) и две чечевицы (13). На стержне через

10 мм нанесены кольцевые нарезки, позволяющие точно определить расстояние между опорными призмами. Опорные призмы и чечевицы можно перемещать вдоль оси стержня и фиксировать в любом положении. Фиксирующие воротки размещены так, чтобы при помощи кольцевых нарезок их можно было наглухо зафиксировать. Нижний кронштейн (5) вместе с фотоэлектрическим датчиком можно перемещать вдоль колонки и фиксировать в произвольном положении.

Для подготовки установки к работе необходимо проделать следующие операции:

- при отжатой кнопке "сеть" подсоедините шнур электропитания к розетке ~220 В;

- нажмите кнопку '"СЕТЬ" и убедитесь в том, что все индикаторы измерителя показывают цифру ноль и горит лампочка фотоэлектрического датчика;

- отгоризонтируйте установку с помощью регулируемых ножек так, чтобы маятник при колебаниях не задевал за фотоэлектрический датчик, но при этом прерывал световой поток в датчике.

Установка позволяет провести прямые измерения периода колебаний математического и оборотного маятников. Для измерения периода колебаний поворотом кронштейна (4) и перемещением кронштейна (5) установите маятник таким образом, чтобы шарик математического маятника или стержень оборотного маятника в положении равновесия прерывал световой поток в фотоэлектрическом датчике (6), но при колебаниях не задевал за датчик. Затем отклоните маятник на угол ~10° от положения равновесия и отпустите его без толчка. Пропустив несколько колебаний, нажмите кнопку "СБРОС" на "лицевой панели прибора (10). При этом запускаются миллисекундомер и счетчик числа полных колебаний маятника. Обычно измеряется время 10 полных колебаний. В этом случае после появления на счетчике периодов цифры «9» нажимается кнопка "СТОП", и отсчет времени прекращается после завершения 10 колебаний. Период колебаний маятника, очевидно, равен (Т = t/10), где t - показания миллисекундомера. Повторный запуск миллисекундомера и счетчика периодов осуществляется нажатием кнопки "СБРОС".

Методика измерений

Описание любой экспериментальной ситуации, в том числе и колебаний маятника, дается теоретической моделью. При разработке модели, естественно, учитывают только наиболее существенные для данной ситуации эффекты и пренебрегают влиянием многих, реально имеющих место факторов. Ответить на вопрос: насколько хорошо теоретическая модель описывает экспериментальную ситуацию, можно только сопоставляя предсказания теории с экспериментальными данными.

Наблюдения за колебаниями математического и оборотного маятников на данной установке показывают, что за время 20 - 30 периодов амплитуда их колебаний заметно не уменьшается. Это означает, что диссипативными силами, т.е. силами трения, сопротивления воздуха и т. д., приводящими к затуханию колебаний, в данном случае можно пренебречь. Кроме того, можно предположить, что колебания математического и оборотного маятников являются малыми. При этих условиях теория дает следующее выражение для периода колебаний оборотного маятника (см. Приложение 1):

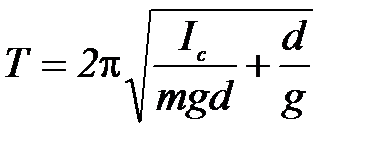, (1)

где I_с – момент инерции маятника относительно оси, проходящей через его центр масс; m – масса маятника; g – ускорение свободного падения; d – расстояние от оси качаний до центра масс маятника.

В случае математического маятника формулa (1) принимает вид:

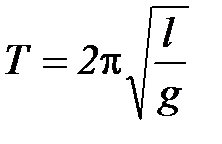, (2)

где l– длина математического маятника.

Формулы (1) и (2) являются основными для данной работы, так как позволяют определить ускорение свободного падения g по измеренным значениям T, d, l, m. Однако они справедливы только в том случае, если колебания маятников являются малыми.

Внимание: Перед началом измерений необходимо определить диапазон амплитуд, в пределах которых колебания можно считать малыми. Поскольку данная установка не позволяет измерять углы отклонения маятника от положения равновесия, их нельзя использовать в качестве критерия малости колебаний. Реализация этого критерия может быть осуществлена следующим образом.

Отклоните математический или оборотный маятник на угол φ₁ ~ 10^о и измерьте период его колебаний Т₁ в соответствии с процедурой, описанной выше. Затем, уменьшив начальное отклонение маятника в 1,5-2 раза, опять определите период его колебаний Т₂. Относительная погрешность измерения времени на данной установке

.

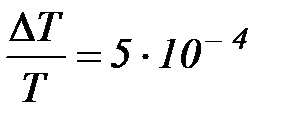С другой стороны, период колебаний маятника не превышает 2 с. Поэтому если |T₁ – T₂| ≤ 0,001, то в пределах точности измерений T₁ = T₂, и для дальнейших измерений можно выбирать любое начальное отклонение маятника, меньшее φ₁. Если же |T₁ – T ₂| > 0,001, то необходимо еще уменьшить начальное отклонение маятника, сравнить измеренный при этом период колебаний с Т₂ и т. д.