Задание 1. Определение момента инерции рамки (Iр) и коэффициента упругих сил кручения (C).
1. Определите период колебаний рамки без закреплённых в ней тел (Т1) по методике, описанной выше.
Теория даёт следующее выражение для периода:
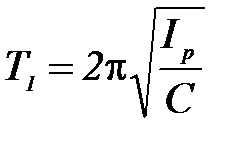, (1)
где Iр – момент инерции рамки без закреплённых в ней тел;
С – коэффициент упругих сил кручения;
2. Измерьте период колебаний рамки с кубом (Т2).
Закрепите в рамке эталонный куб в центрах противоположных граней и найдите период Т21 колебаний системы (рисунок 2). Повторите измерения для остальных двух пар противоположных граней, найдя Т22; Т23. Усредняя найденные значения, найдите период Т2 колебаний рамки с закрепленным в ней эталонным кубом: Рисунок 2
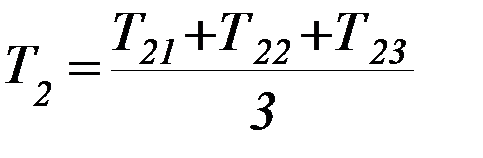
Теория даёт следующее выражение для периода колебаний рамки с закреплённым в ней кубом:
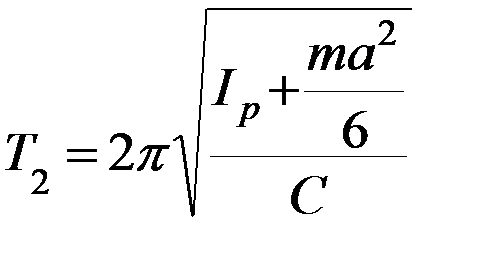, (2)
где m – масса куба; а – сторона куба (указаны на рабочем месте), С – постоянная упругих сил кручения.
3. Из системы уравнений (1) и (2) найдите Iр и С.
4. Рассчитайте относительную погрешность определения момента инерции рамки (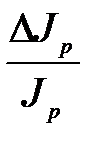 
) и коэффициента упругих сил кручения ( 
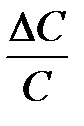) как сумму относительных погрешностей прямым образом измеренных величин.
Относительные погрешности прямым образом определяемых величин (m, T, a) принять равными: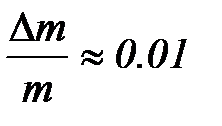 
; 
; 
.
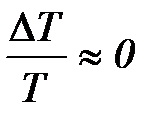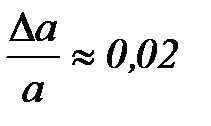Задание 2. Определение момента инерции груза (Iгр)
1. Измерьте период колебаний рамки со стержнем (Т3). Для этого закрепите в рамке длинный стержень так, чтобы ось колебаний проходила через его центр (рисунок 3) и измерьте период Т3 колебаний рамки со стержнем. Убедитесь, что период Т3 практически не зависит от угла между плоскостью рамки и стержнем. Рисунок 3
Если эта зависимость присутствует, следует более аккуратно крепить стержень в рамке, соблюдая перпендикулярность стержня к оси колебаний и повторить измерение Т3.
Вследствие аддитивности момента инерции согласно теории имеем:
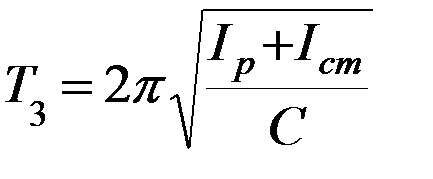, (3)
где Iст – момент инерции стержня;
2. Из формулы (3), зная Ip из предыдущего задания, найдите момент инерции Iст.
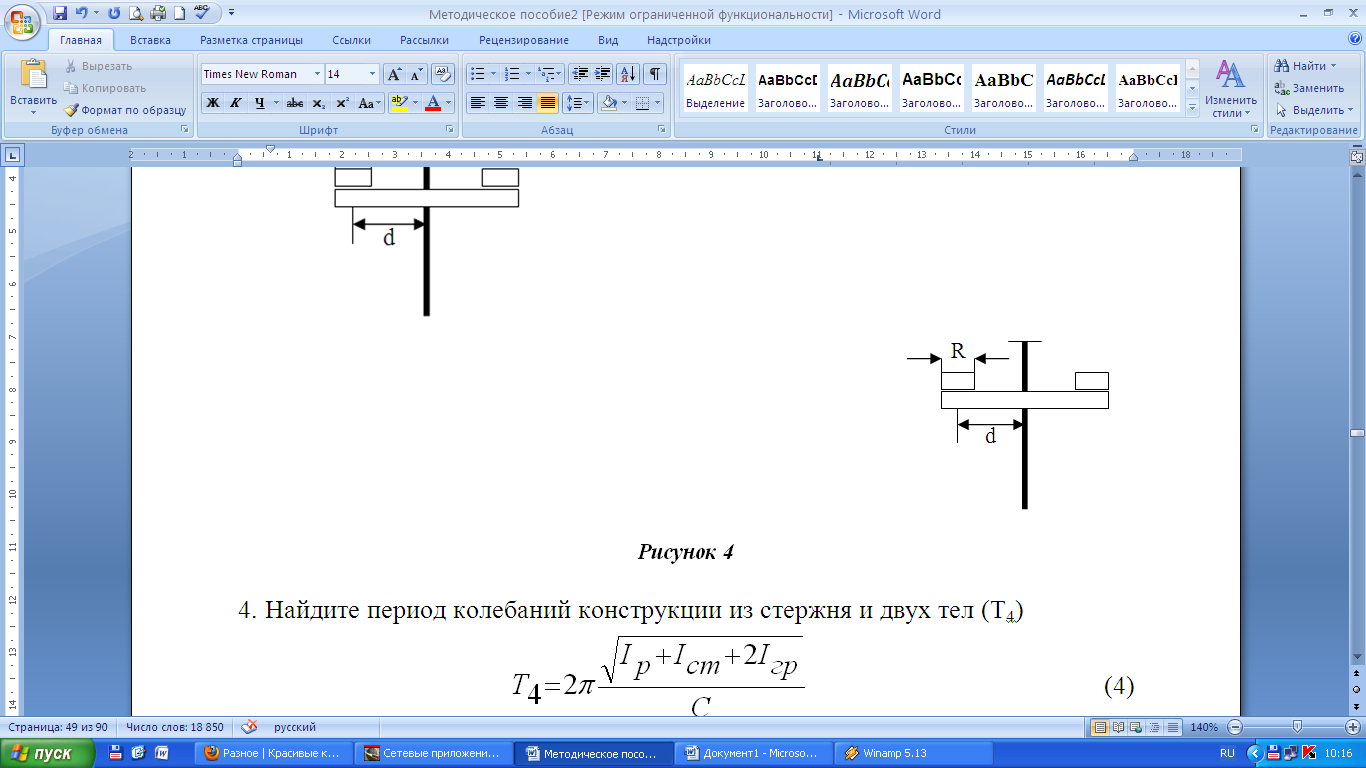
3. Прикрепите к стержню, закрепленному в рамке, симметрично два одинаковых тела с помощью штырьков, имеющихся на этих телах, на расстоянии d от стержня (рис. 4). Рисунок 4
4. Найдите период колебаний конструкции из стержня и двух тел (Т4) Рисунок 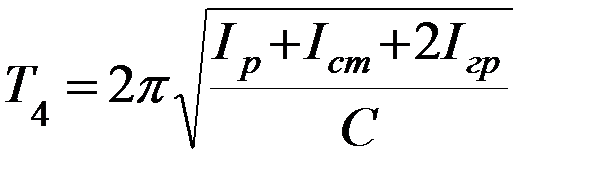4
(4)
5. Из формулы (4) найдите момент инерции груза (Iгр) и сравните его с теоретическими значениями, найденными по формулам (5) и (6). По теореме Гюйгенса-Штейнера (см. Приложение):
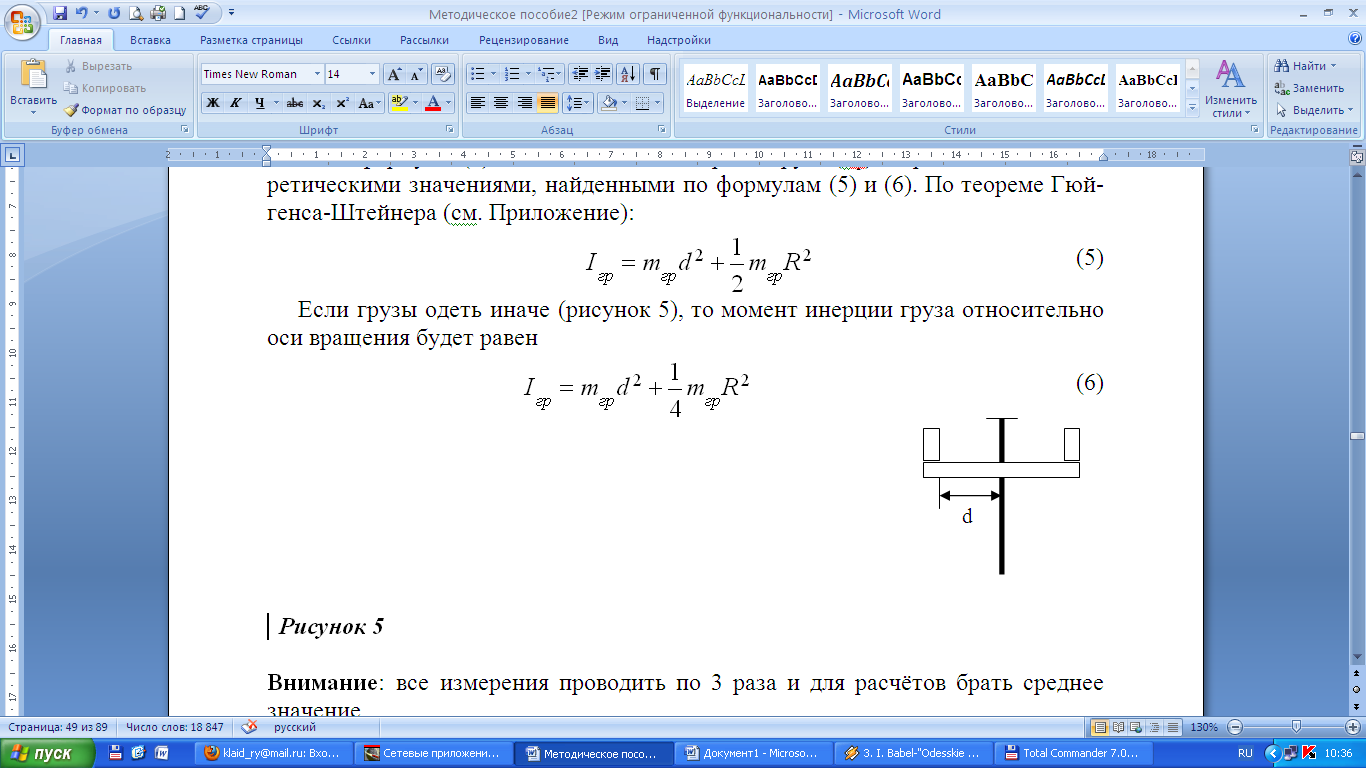
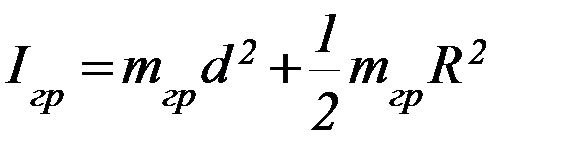, (5)
где R – радиус груза.
Если грузы одеть иначе (рисунок 5), то момент инерции груза относительно оси вращения будет равен:
| Рисунок 5 |
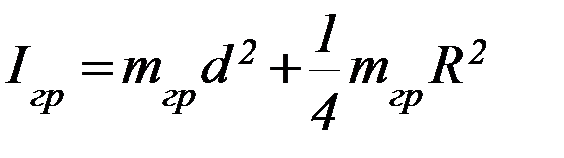(6)
Внимание: все измерения проводить по 3 раза и для расчётов брать среднее значение.
6. Рассчитайте относительную погрешность определения момента инерции груза (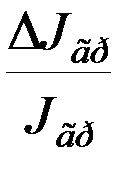 
) как сумму относительных погрешностей момента инерции рамки и коэффициента упругих сил кручения.
Относительной погрешностью определения периода в силу малости можно пренебречь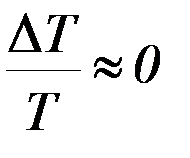 
. Относительные погрешности момента инерции рамки и коэффициента упругих сил кручения взять из предыдущего задания.
Дата добавления: 2015-11-18; просмотров: 1633;