Изучение законов динамики вращательного

Движения твердого тела вокруг неподвижной

Оси на маятнике обербека

Цель работы:

– экспериментальная проверка зависимостей между физическими величинами, характеризующими вращение твердого тела вокруг неподвижной оси.

Приборы и принадлежности:

– маятник Обербека; комплект перегрузов; миллисекундомер.

Описание установки

Рисунок 1 – Общий вид установки

Маятник Обербека представляет собой крестовину, на оси которой закреплены два блока радиусами r₁ и r₂. На диски может наматываться нить, причём один конец нити прикрепляется к диску, а на другой подвешен груз m₁, состоящий из основного груза, на который могут помещать добавочные грузы. Поступательное движение груза вниз вызывает вращательное движение крестовины с блоками вокруг неподвижной горизонтальной оси. На четырех взаимно перпендикулярных стержнях симметрично расположены грузы массой m. Их можно установить на любом заданном расстоянии r от оси вращения. Маятник с помощью неподвижного кронштейна установлен на вертикальной колонне, на которой нанесена миллиметровая шкала для подсчета длины перемещения грузов. На вертикальной колонне (1) прикреплены два кронштейна: нижний (2) неподвижный и верхний (3) подвижный. Подвижный кронштейн (3) можно перемещать вдоль колонны (1) и фиксировать его в любом положении, задавая таким образом расстояние Н,которое проходят грузы. Установка снабжена двумя фотоэлектрическими датчиками (4 и 5), вырабатывающими электрические импульсы соответственно начала и конца измерения времени движения грузов. Маятник с грузами удерживается в состоянии покоя с помощью тормозного электромагнита. На основании колонны жестко закреплен миллисекундомер (6), к которому подключены фотодатчики. Само основание прибора снабжено регулируемыми ножками (7), обеспечивающими горизонтальную установку прибора.

На установке можно провести прямое измерение времени движения груза массой m₁ на пути Н и получить таким образом множество значений времени при различных m₁, H, r и радиусах намотки r₁иr₂ и различных положениях грузов m.

Ясно, что проведение измерений времени при всех возможных комбинациях указанных величин – нереальная задача. Кроме того, неясно, что с результатами делать дальше и что с их помощью можно определить.

Ответы на последние вопросы дает теоретическая модель экспериментальной ситуации. Она же позволяет составить план измерений и обработки результатов.

Любая теоретическая модель дает приближенное описание экспериментальной ситуации, поскольку пренебрегает влияниям многих реально имеющих место эффектов.

Внимание! Для отчета по работе необходимо изучить также материал приложений.

В этой модели считается, что трение в оси блока (8) отсутствует, этот блок невесом, а момент сил трения Μ_тр, в оси блока с крестовиной не зависит от угловой скорости вращения. В этих условиях ускорение груза массой m постоянно на всем отрезке Ни равно:

,

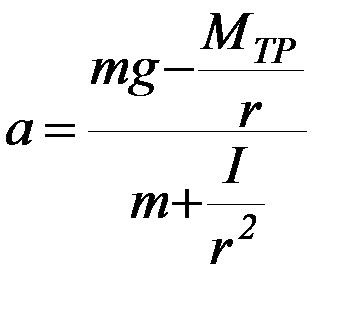где r – радиус намотки, I – момент инерции блока с крестовиной (r = r₁ либо r₂,

I – определяется положением грузов массой mкаждый и моментом инерции блока без грузов I_о ( ).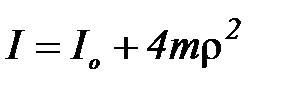

С другой стороны, на основании кинематических соображений, если а – постоянная величина, то ,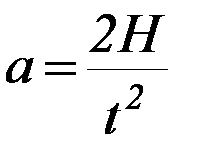

где Н – задаваемое перемещение груза, t– измеренное время его движения.

Имеем: 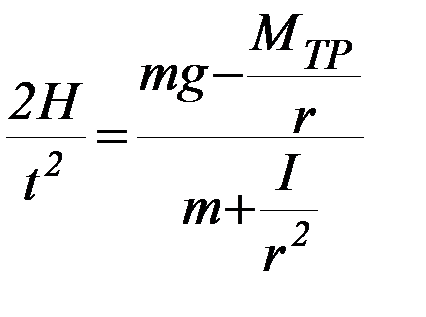(1)

Тогда формула (1) является основной для работы в рамках теоретической модели.