II начало термодинамики. Энтропия. Термодинамическая трактовка

Второе начало термодинамики играет важнейшую роль в понимании процессов и явлений природы.

Впервые II Начало было, фактически, сформулировано пусть в несовершенной форме, еще в начале 19-го века и в этом виде понятно любому человеку, поскольку он сталкивается с ним в своем повседневном опыте.

Так, в 1811 г. Жан-Батист Фурье сформулировал закон теплопроводности, согласно которому количество теплоты, которое переносится в единицу времени через единицу площади поверхности вдоль какого-либо направления (т.е. через единицу длины), прямо пропорционально величине изменения температуры вдоль этого направления.

,

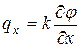где q – поток тепла в направлении х на единицу длины за единицу времени, j(x,y,t) – распределение температуры.

При этом количество теплоты переносится от участков с большей температурой в направлении участков с меньшей температурой и никогда наоборот.. Теплопроводность приводит к все большему выравниванию температур до тех пор, пока распределение температуры во всех точках пространства рассматриваемой изолированной системы не станет одинаковым.

Фактически, закон теплопроводности уже выходил за рамки классической ньютоновской механики по той причине, что описывал необратимый процесс, а все законы ньютоновской механики являются обратимыми, инвариантными относительно направления времени.Так в науку вошло понятие необратимости, дальнейшее развитие которого связано с работой С. Карно по исследованию действия паровых машин.

Процесс (1)-(2): от нагретого тела с температурой Т₁ тепло подводится (при постоянной температуре) к газу, который расширяется при постоянной температуре.

Процесс (2)-(3): газ расширяется в условиях полной теплоизоляции сосуда от окружающей среды.

Процесс (3)-(4): тепло отнимается при изотермическом процессе и отдается холодному телу с температурой Т₂.

Процесс (4)-(1), замыкающий цикл соответствует адиабатическому сжатию.

Пусть в процессе (1)-(2) газ получает от холодильника теплоту Q₁, а холодильнику отдает теплоту Q₂. Тогда за весь цикл он получит теплоту Q₁ – Q₂ , равную совершенной работе А.

Тогда КПД теплового двигателя, работающего по циклу Карно:

КПД = A₁/Q₁ = (Q₁ – Q₂)/Q₁ .(1)

Можно показать, что Q₁/Q₂ = T₁/T₂ (для случая идеального газа).

Соотношение полученного тепла к отданному теплу равно отношению абсолютных температур нагревателя и холодильника.

Тогда

КПД = (Q₁ – Q₂)/Q₁ = 1 – Q₂/Q₁ = 1 – T₂/T₁ = (T₁ – T₂)/T₁. (2)

Получается, что в случае цикла Карно КПД при превращении тепла в работу зависит только от температуры нагревателя и холодильника (таким образом, процесс не зависит ни от количества используемого газа, ни от начальных значений давления или объема).

Вспомним, что площадь, ограниченная криволинейным четырехугоугольником, изображающим идеальный цикл Карно, равна полной работе, совершаемой газом, а площадь под кривыми (1)-(4) и (4)-(3) - работе, совершенной над газом, т.е. затраченной.

Сущность второго начала термодинамики.Возможность построения машины без холодильника, т.е. с КПД = 1, которая могла бы превращать в работу всю теплоту, заимствованную у теплового резервуара, не противоречит закону сохранения энергии. Такая машина, по сути, была бы аналогична perpetuum mobile (вечному двигателю), так как могла бы производить работу за счет практически неисчерпаемых источников энергии, содержащихся в воде морей, океанов, атмосфере и недрах Земли. Такую машину У. Оствальд (1853-1932) назвал perpetuum mobile II рода ( в отличие от perpetuum mobile I рода – вечного двигателя, производящего работу из ничего). Карно же исходил из невозможности вечного двигателя, опираясь на многочисленные опытные факты и утверждая, что в любом непрерывном процессе превращения теплоты от горячего нагревателя в работу непременно должна происходить отдача тепла холодильнику.

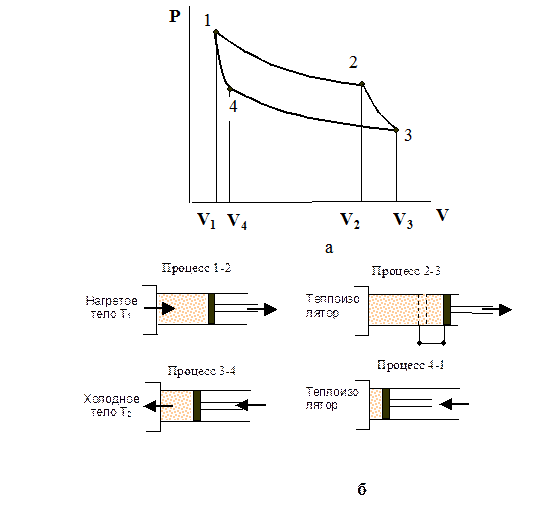Рис. 1

 

Таким образом, здесь проявляется общее свойство теплоты – уравнивание температурной разницы путем перехода от теплых тел к холодным. Это положение Клаузиус и предложил назвать «Вторым началом механической теории теплоты». Если Первое начало термодинамики утверждает закон сохранения энергии, ее баланс, то Второе начало определяет направления превращения энергии, и если в предыдущей лекции Первому началу была сопоставлена роль «бухгалтера», то Второе начало выступает скорее как «диспетчер», определяющий направление энергетических потоков.

 

Для идеальной машины Карно следует

Q₁/T₁ = Q₂/T₂ или Q₁/T₁ - Q₂/T₂ = 0. (Q₁ –теплота, сообщаемая газу, Q₂ – теплота, отводимая).

Для того, чтобы учесть, что Q₂ отдается холодильнику, берем его со знаком “ - “. Тогда имеем:

Q₁/T₁ + Q₂/T₂ = 0

DQ₁ /Т₁ + DQ₂/Т₂ = 0

Как видим, эта запись напоминает закон сохранения, но при этом появляется некоторая “интересная” величина DQ /Т.

Так в физике появилось новое понятие «энтропия» (<entropia греч. поворот, превращение). Ввел его в 1865 г. Клаузиус. Он предположил, что есть некоторая величина S, которая, подобно энергии, давлению, температуре, характеризует состояние газа. Когда к газу подводится некоторое количество DQ, то S возрастает на величину DS= DQ /Т.

Ранее говорилось о том, что раньше не делалось различий между понятиями теплота и температура.

После введения понятия энтропии стало ясно, где пролегает эта граница. Дело в том, что нельзя говорить о том, что в теле заключено какое-то количество теплоты. Теплота может передаваться от тела к телу, переходить в работу, возникать при трении, но при этом она (теплота) не является сохраняющей величиной. Поэтому теплота определяется в физике не как вид энергии, а как мера изменения энергии. А вот энтропия в обратимых процессах (в частности в идеальном цикле Карно) сохраняется. Энтропия, таким образом, характеризует состояние системы.

Можно провести некоторую аналогию с потенциальной энергией. Действительно, так же как каждому уровню высоты над поверхностью Земли отвечает своя потенциальная энергия, так и каждому состоянию термодинамической системы отвечает своя энтропия.

Как работа в поле тяжести (потенциальном поле) не зависит от вида пути, а зависит только от изменения потенциальной энергии, так и энтропия не зависит от вида процесса и определяется исключительно изменением состояния системы как конечным результатом процесса.

Все это означает, что энтропия системы может рассматриваться как функция состояния системы, т.к. изменение ее не зависит от вида процесса, а определяется лишь начальным и конечным состоянием системы.

Итак, для обратимых процессов имеем DS=сonst. , т.е. энтропия изолированной системы в случае обратимых процессов постоянна.

Заметим, что для осуществления необратимого процесса необходимо добиться очень медленного расширения или сжатия рабочего тела, чтобы изменения системы представляли собой последовательность равновесных состояний. В таком цикле совершение любой полезной работы потребует практически бесконечно большого времени. Чтобы получить работу за короткие, т.е. приемлемые промежутки времени (хорошую мощность), приходится «уходить» от идеального цикла. Это приведет к неодинаковости температуры на разных участках цикла, к перетеканию тепла от более горячих участков к менее горячим и, следовательно, к возрастанию энтропии DS>0.

Понятие энтропии позволяет определить направление протекания процессов в природе, поскольку тот факт, что энтропия изолированной системы не может убывать, а только возрастает, является отражением того, что в природе существуют процессы, протекающие только в одном направлении - в направлении передачи тепла от более горячих тел к менее горячим.

Теперь мы можем полностью определиться с формулировками II Начала термодинамики. Существует ряд его формулировок:

В природе невозможны такие процессы, единственным конечным результатом которых был бы переход тепла от менее нагретого к более нагретому.

КПД любой тепловой машины всегда <100%, т.е. невозможен вечный двигатель (perpetuum mobile) II рода (т.к. невозможно построить тепловую машину, работающую не за счет перепада теплоты, а за счет теплоты одного нагревателя.

Энтропия изолированной системы не убывает (т.е. при протекании обратимых процессов энтропия постоянна, а при необратимых процессах она возрастает). Энтропия системы, находящейся в равновесном состоянии максимальна и постоянна.