Приложение. Момент инерции и его вычисление.

Пусть твёрдое тело вращается вокруг оси Z (рисунок 6). Его можно представить как неизменную с течением времени систему разных материальных точек m_i, каждая из которых движется по окружности радиусом r_i, лежащей в плоскости, перпендикулярной оси Z. Угловые скорости всех материальных точек одинаковы. Моментом инерции тела относительно оси Z называется величина:

,

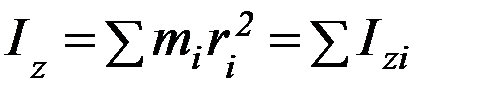где 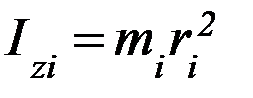– момент инерции отдельной материальной точки относительно оси ОZ. Из определения вытекает, что момент инерции – аддитивная величина, т. е. момент инерции тела, состоящего из отдельных частей, равен сумме моментов инерции частей.

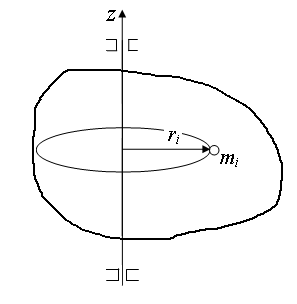
Рисунок 6

Очевидно, [I] = кг×м². Важность понятия момента инерции выражается в трёх формулах:

; ; .

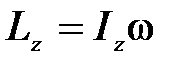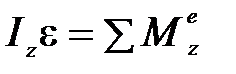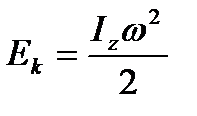Первая из них выражает момент импульса тела, которое вращается вокруг неподвижной оси Z (полезно эту формулу сравнить с выражением для импульса тела P = mV_c, где V_c – скорость центра масс). Вторая формула носит название основного уравнения динамики вращательного движения тела вокруг неподвижной оси, т.е., иначе говоря, второго закона Ньютона для вращательного движения (сравним с законом движения центра масс: 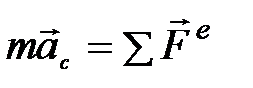). Третья формула выражает кинетическую энергию тела, вращающегося вокруг неподвижной оси (сравним с выражением для кинетической энергии частицы 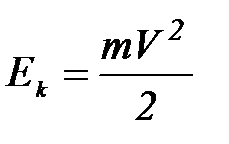). Сравнение формул позволяет сделать вывод о том, что момент инерции во вращательном движении играет роль, аналогичную массе в том смысле, что чем больше момент инерции тела, тем меньше угловое ускорение при прочих равных условиях оно приобретает (тело, образно говоря, труднее раскрутить). Реально вычисление моментов инерции сводится к вычислению тройного интеграла и может быть произведено лишь для ограниченного числа симметричных тел и лишь для осей симметрии. Количество осей, вокруг которых может вращаться тело, бесконечно велико. Среди всех осей выделяется та, которая проходит через замечательную точку тела – центр масс (точку, для описания движения которой достаточно представить, что вся масса системы сосредоточена в центре масс и к этой точке приложена сила, равная сумме всех сил). Но осей, проходящих через центр масс, также бесконечно много. Оказывается, что для любого твёрдого тела произвольной формы существуют три взаимно перпендикулярных оси С_х, С_у, С_z, называемые осями свободного вращения, обладающие замечательным свойством: если тело закрутить вокруг любой из этих осей и подбросить вверх, то при последующем движении тела ось останется параллельной самой себе, т.е. не будет кувыркаться. Закручивание вокруг любой другой оси этим свойством не обладает. Значение моментов инерции типичных тел относительно указанных осей приведено ниже. Если ось проходит через центр масс, но составляет углы a, b, g с осями С_х, С_у, С_z соответственно, то момент инерции относительно такой оси равен

I_c = I_cxcos²a + I_cycos²b + I_czcos²g (*)

Рассмотрим кратко вычисление момента инерции для простейших тел.

1. Момент инерции длинного тонкого однородного стержня относительно оси, проходящей через центр масс стержня и ему перпендикулярной.

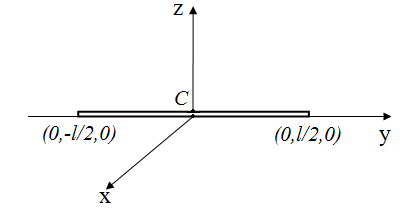Пусть т – масса стержня, l – его длина.

,

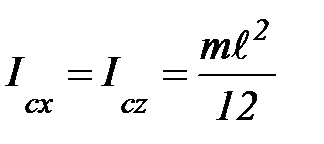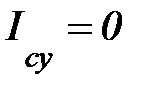
Индекс «с» у момента инерции I _c означает, что это момент инерции относительно оси, проходящий через точку центра масс (центр симметрии тела), C(0,0,0).

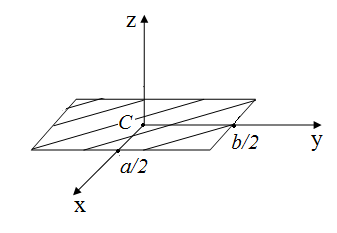
2. Момент инерции тонкой прямоугольной пластинки.

; ;

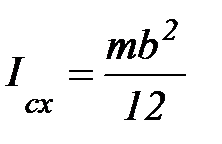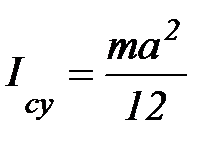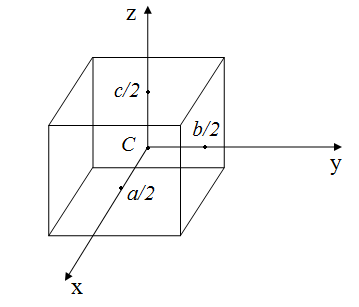
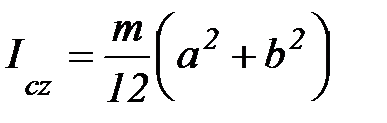
3. Момент инерции прямоугольного параллелепипеда.

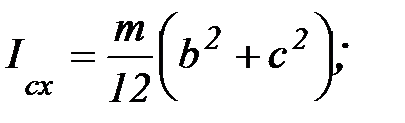
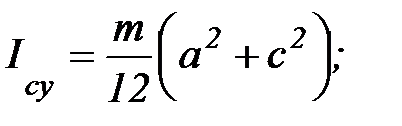
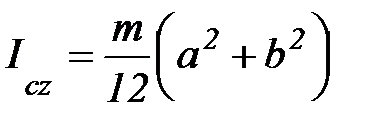, т. С(0,0,0)

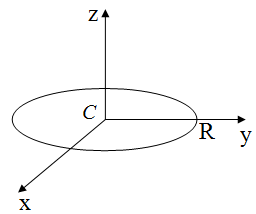4. Момент инерции тонкого кольца.

;

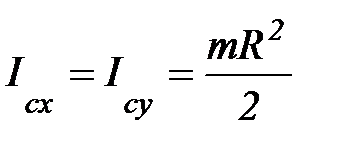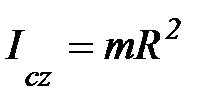, т. С(0,0,0)

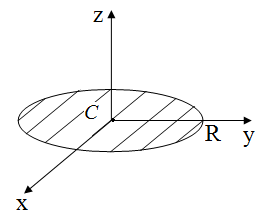5. Момент инерции тонкого диска.

В силу симметрии

; ;

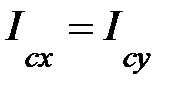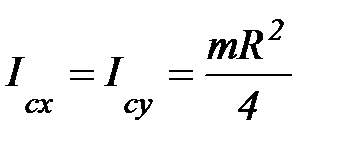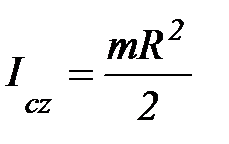
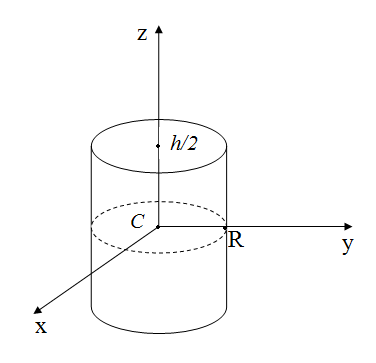6. Момент инерции сплошного цилиндра.

;

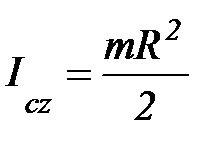В силу симметрии:

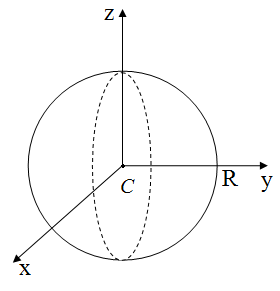
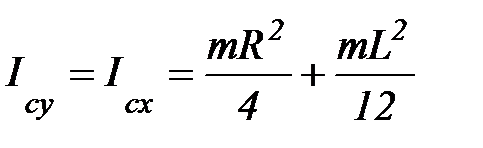
7. Момент инерции сплошного шара.

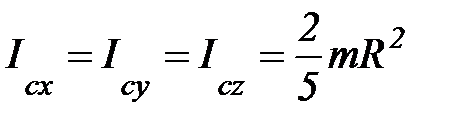, т. С(0,0,0)

8. Момент инерции сплошного конуса.

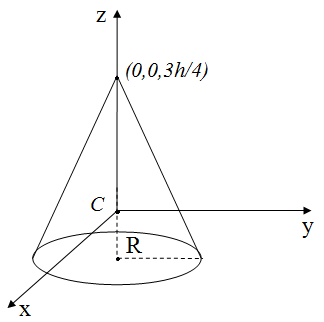
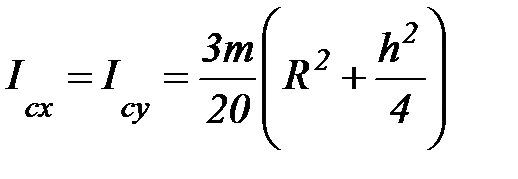
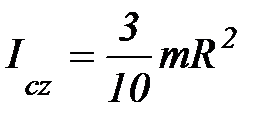, т. С(0,0,0)

где R – радиус основания, h – высота конуса.

Напомним, что cos²a + cos²b + cos²g = 1. Наконец, если ось О не проходит через центр масс, то момент инерции тела может быть вычислен с помощью теоремы Гюйгенса Штейнера

I_о = I_с + md², (**)

где I_о – момент инерции тела относительно произвольной оси, I_с – момент инерции относительно параллельной ей оси, проходящей через центр масс,
m – масса тела, d – расстояние между осями.

Процедура вычисления моментов инерции для тел стандартной формы относительно произвольной оси сводится к следующему:

1. 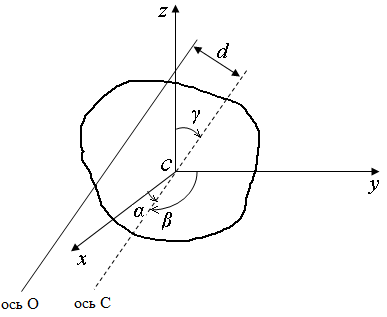Проведите ось, параллельную данной оси О и проходящую через центр масс.

2. Находите углы a, b, g между осями С_х, С_у, С_z, совпадающими с осями вращения и показанными на рисунках, и осью С и по формуле (*) находите I_c.

3. По формуле (**) находите искомый момент инерции.

В качестве примера определим момент инерции цилиндра в ситуации, показанной на рисунке (см. ниже).

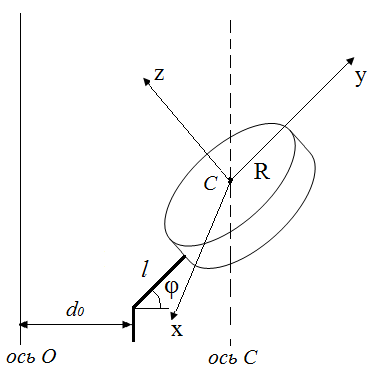Здесь ось О лежит в плоскости YСZ, ось OX перпендикулярна этой плоскости, поэтому

; ; ;

,

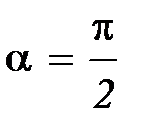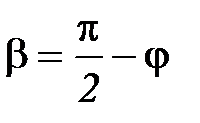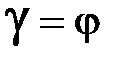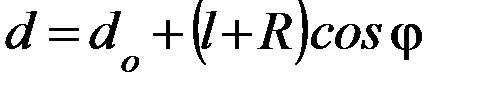тогда:

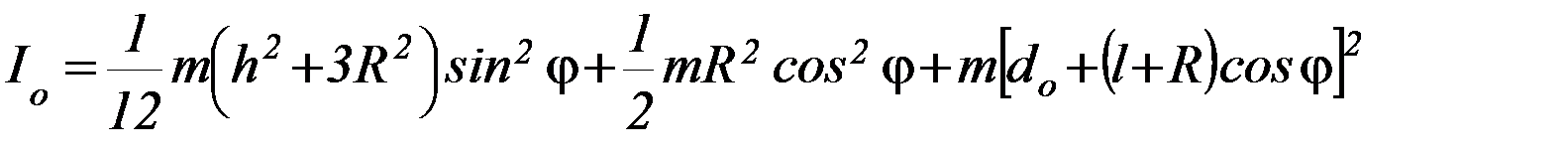
Заметим, наконец, что в реальной практике приходится определять момент инерции тел достаточно сложной формы. Это связано в частности с тем, например, что напряжения, возникающие в упругом теле при изгибе и кручении, зависят от моментов инерции, а значения этих напряжений необходимы во многих задачах. Вычисление моментов инерции в таких случаях достаточно затруднительно, поэтому разумно использовать экспериментальные методы. Один из таких методов и рассмотрен в данной работе.