Гармонические колебания. Маятники и колебательный контур. Затухающие и вынужденные колебания. Резонанс

Колебаниями называются движения или процессы, в той или иной степени повторяющиеся во времени. Можно сказать, что весь мир пронизан колебательными процессами: пульсирует излучение звезд, вращаются планеты Солнечной системы и электроны в атоме колеблются разнообразные маятники, ритмичные колебания происходят в живых организмах и т. д.

Большое значение имеют периодические колебания (процессы, повторяющиеся через равные промежутки времени, минимальный из которых назван периодом Т), которые можно представить в виде суммы простых гармонических колебаний (периодические колебания, происходящие по закону синуса или косинуса) с циклическими частотами, кратными основной частоте 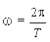(гармонический анализ).

Колебания являются свободными (собственными), если они совершаются за счет первоначально полученной энергии при отсутствии последующих воздействий на колебательную систему. Частоту свободных колебаний называют собственной частотой.

Характерным примером гармонических колебаний является проекция точки, движущейся равномерно по окружности (w₀ = const), на линию, лежащую в плоскости движения точки, рис. 9.1.

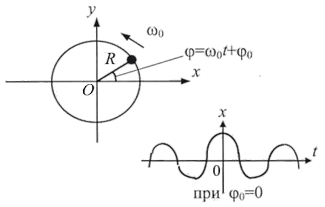
Рис. 9.1

Такая система описывается уравнением типа

х = Acos(w₀t + j₀), (9.1)

где А ¾ амплитуда (модуль наибольшей величины отклонения системы от положения равновесия, в нашем случае А = R), w₀ ¾ собственная круговая частота, t + j₀) и j₀ ¾ соответственно фаза и начальная фаза колебаний (в начальный момент, когда t = 0). Графическое представление уравнения (9.1) показано на рис. 9.1.

Первая и вторая производные по времени от х также изменяется по гармоническому закону:

Волны

Прямым следствием колебаний являются волны, под которыми понимают изменения некоторой совокупности физических величин (полей), способные перемещаться, удаляясь от места их возникновения, или совершать колебания в ограниченной области пространства.

Волны не обязательно связаны с наличием вещества. Например, электромагнитные волны в вакууме представляют собой взаимосвязанные изменения электрических и магнитных полей.

Если в качестве примера колеблющееся тело поместить в упругую среду, то оно будет воздействовать на соседние частицы среды и приводить их в колебательное движение. Общее колебание распространяется в среде с некоторой скоростью v. Процесс распространения колебаний в упругой среде и называется волной.

Волны, образованные внешним воздействием, приложенным к открытой среде, то есть среде, не имеющей внешних границ, называются бегущими. Геометрическое место точек, колеблющихся в одинаковой фазе называется волновой поверхностью. Простейшие формы волновой поверхности ¾ это плоскость или сфера, соответственно волна называется плоской или сферической.

Классические плоские бегущие волны от гармонического источника колебаний описываются уравнением¹.

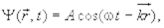(9.14)

где 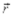¾радиус-вектор, характеризующий положение колеблющейся точки волны относительно начала координат, 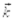¾волновой вектор перпендикулярный плоскому фронту волны и равный 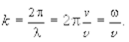В данном случае v¾фазовая скорость распространения волны (скорость перемещения фиксированного значения фазы, колебаний), l¾длина волны, это ее пространственный период, то есть расстояние между двумя ближайшими точками волны, имеющими одинаковую фазу колебаний.

Геометрическое место точек, до которых доходят колебания к моменту времени t, называется волновым фронтом. У плоских волн он имеет вид плоскости, у сферических ¾ сферы.

Волны бывают поперечными и продольными. В поперечных волнах колебания происходят в направлении перпендикулярном к направлению распространения волны (волны в натянутой веревке, электромагнитные волны и т. д.), в продольных ¾ в направлении распространения волны (звуковые волны, волны в сжатой и затем отпущенной пружине и т. д.).

В течение одного периода колебательный процесс распространяется на расстояние, равное длине волны, поэтому

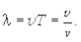(9.15)

Пример. На рис. 9.5 показана качественная картина распространения поперечной бегущей волны вдоль веревки с небольшими шарами (вдоль оси х), возникающей в результате гармонических колебаний первого шара.

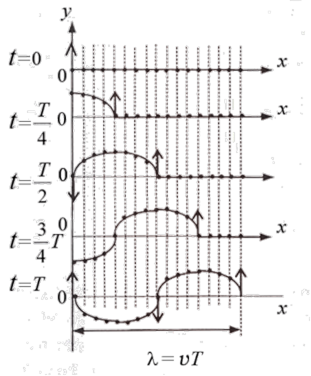
Рис. 9.5

Уравнение волны, согласно (9.14), в данном случае имеет вид 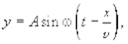так как колебания шаров в точке х отстают во времени на 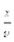от колебаний первого шара в т. х =0.

Механические поперечные волны возникают только в среде, обладающей сопротивлением сдвигу. Шары, которые отстоят друг от друга на расстоянии l = vТ колеблются в одинаковой фазе, это расстояние называется длиной волны.

Распространение бегущих волн происходит с переносом энергии и импульса. Скорость распространения электромагнитных волн в вакууме 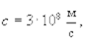в среде 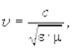где e, m¾диэлектрическая и магнитная проницаемость среды.

На рис. 9.6 показан пример распространения электромагнитной волны (распространение электромагнитных колебаний в пространстве с конечной скоростью v).

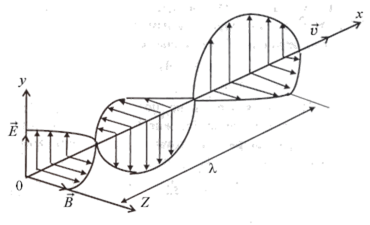
Рис. 9.6

Шкала электромагнитных волн в зависимости от длины волны условно делится на диапазоны:

радиоволны ® l = 30 км - 1 мм

инфракрасные волны ® l = 1 мм - 750 нм

световые волны ® l = 750 нм - 400 нм (видимый диапазон)

ультрафиолетовые волны ® l = 400 нм - 5 нм

рентгеновское излучение ® l = 5 нм - 4 пм

гамма-излучение ® l £ 4 пм

¹для волн, распространяющихся в упругой среде, 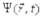представляет собой, смещение колеблющейся частицы в зависимости от координат и времени.