Лабораторна робота 127. Визначення коефіцієнта тертя кочення
Завдання :вивчити явище тертя ковзання та кочення шляхом експериментального визначення коефіцієнтів тертя кочення різних матеріалів.
Приладдя: лабораторна установка; секундомір; лінійка; металева тригранна призма; набір досліджуваних матеріалів : сталь, латунь, мідь, алюміній, оргскло, вакуумна гума.
Теоретичний матеріал: сили тертя; класифікація сил тертя; тертя ковзання і кочення; момент сили; центр мас; закон збереження енергії.
Література:
1. Р.5. §. 5.1;
2. Р.2. §. 2.11 ;
3. §. 12;
4.  §. 20;
§. 20;
5. §. 36.
Опис установки.Основним елементом установки (рис. 1) для визначення коефіцієнта тертя кочення є циліндр 2, розміщений на горизонтальній сталевій плиті 3. На циліндр напресовано обойму, у діаметральних точках якої закріплені два стержні. Стержень 1 є стрілкою шкали; на стержні 5 можна пересувати і закріплювати вантаж 4. Рухому частину установки можна назвати маятником. Відхиляючись від стану рівноваги, маятник починає виконувати згасаючі коливання. Вісь циліндра у разі цього рухається поступально, а циліндр обертається навколо своєї осі. Під циліндр можна підкласти пластинки з різних матеріалів, що дає змогу визначити коефіцієнти тертя кочення для пари матеріалів циліндр – пластинка.
Виведення робочої формули.Під час кочення тіла, що має криволінійну поверхню, по-іншому тілу з плоскою чи криволінійною поверхнею виникає опір, який називається тертям кочення. Природа тертя кочення є інша, ніж природа тертя ковзання. Опір кочення залежить від пружних властивостей матеріалу тіл, кривизни їхніх поверхонь і нормальної сили, яка діє між тілами.
 Розглянемо два тіла: циліндр, розміщений на пластині (рис. 2). Циліндр 1 притискається до пласти 2 силою
Розглянемо два тіла: циліндр, розміщений на пластині (рис. 2). Циліндр 1 притискається до пласти 2 силою 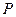 . Оскільки циліндр і пластина не є абсолютно твердими тілами, то в зоні їхнього дотику під дією сили
. Оскільки циліндр і пластина не є абсолютно твердими тілами, то в зоні їхнього дотику під дією сили 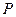 виникає деяка зона змикання. Напруженість у зоні змикання розподіля-ється за еліптичним законом. Рівнодійна напруженості
виникає деяка зона змикання. Напруженість у зоні змикання розподіля-ється за еліптичним законом. Рівнодійна напруженості 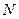 у цьому випадку дорівнює силі
у цьому випадку дорівнює силі 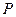 , напрямлена протилежно і діє по одній лінії з нею. Під час кочення циліндра діаграма зміниться (рис. 2, В). На ділянці бc виникає зона наростаючих, а на ділянці aб – зникаючих деформацій. У зоні наростаючих деформацій нормальна напруженість більша, ніж у зоні зникаючих. Рівнодійна напруженості у цьому випадку також дорівнює за значенням вазі циліндра
, напрямлена протилежно і діє по одній лінії з нею. Під час кочення циліндра діаграма зміниться (рис. 2, В). На ділянці бc виникає зона наростаючих, а на ділянці aб – зникаючих деформацій. У зоні наростаючих деформацій нормальна напруженість більша, ніж у зоні зникаючих. Рівнодійна напруженості у цьому випадку також дорівнює за значенням вазі циліндра 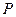 , але зміщена від осі циліндра 0 вперед на величину
, але зміщена від осі циліндра 0 вперед на величину 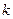 (цю величину називають коефіцієнтом тертя кочення ). Отже, під час кочення тіла обертання потрібно переборювати момент сили тертя
(цю величину називають коефіцієнтом тертя кочення ). Отже, під час кочення тіла обертання потрібно переборювати момент сили тертя
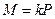 (1)
(1)
У разі цього треба, щоб момент сили (дорівнював силі тертя спокою), який діє в горизонтальній площині на висоті осі циліндра, дорівнював моментові сили тертя кочення :
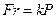 , (2)
, (2)
або
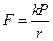 (3)
(3)
де r – радіус циліндра.
Відхилення стрілки за шкалою (рис. 3) складається з двох відхилень:
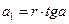 і
і 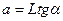 (4)
(4)
де 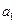 - зміщення осі циліндра внаслідок його поступального руху;
- зміщення осі циліндра внаслідок його поступального руху; 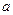 - відхилення, спричинене обертанням циліндра навколо осі;
- відхилення, спричинене обертанням циліндра навколо осі; 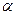 - кут повороту циліндра;
- кут повороту циліндра; 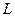 - відстань від осі обертання до шкали. Сумарне відхилення стрілки
- відстань від осі обертання до шкали. Сумарне відхилення стрілки

 .(5)
.(5)
У випадку  можна знехтувати величиною
можна знехтувати величиною 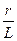 , тоді
, тоді
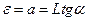 (6)
(6)
Якщо 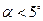 , то для початкового відхилення (
, то для початкового відхилення ( 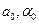 ) і відхилення після
) і відхилення після 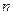 повних коливань
повних коливань 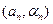 , відповідно
, відповідно
 ;
; 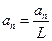 . (7)
. (7)
Зменшення кута відхи-лення за відому кількість періодів коливань дає змогу обчислити значення коефіцієнта тертя кочення.
Уважаючи, що коефіцієнт тертя кочення не залежить від швидкості руху маятника, використаємо закон збереження енергії. Для початкового відхилення маятника на кут 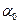 його потенціальну енергію можна записати у вигляді (рис. 4)
його потенціальну енергію можна записати у вигляді (рис. 4)
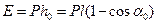 , (8)
, (8)
де 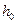 - вертикальне зміщення точки центра мас маятника,
- вертикальне зміщення точки центра мас маятника,  - відстань від осі обертання до його центра мас.
- відстань від осі обертання до його центра мас.
Через один повний період потенціальна енергія маятника
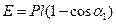 , (9)
, (9)
де  - кут, на який відхилився маятник через Т секунд.
- кут, на який відхилився маятник через Т секунд.
Зменшення потенціальної енергії за один період
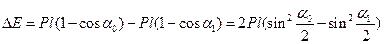 , (10)
, (10)
Для малих кутів відхилення маятника ( 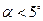 )
) 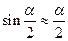 , тому
, тому 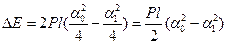 . (11)
. (11)
 Зміна енергії за повний період коливань маятника дорівнюватиме роботі сил тертя кочення (силами опору повітря нехтуємо) :
Зміна енергії за повний період коливань маятника дорівнюватиме роботі сил тертя кочення (силами опору повітря нехтуємо) :
 (12)
(12)
де  - кут відхилення після одного півперіоду коливання;
- кут відхилення після одного півперіоду коливання; 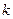 - коефіцієнт тертя кочення. Нехай
- коефіцієнт тертя кочення. Нехай  - зменшення кута відхилення маятника за один півперіод, тоді
- зменшення кута відхилення маятника за один півперіод, тоді
 (13)
(13)
З формул (12) та (13) отримуємо
 (14)
(14)
Порівнявши між собою вирази (11) і (14), одержимо:
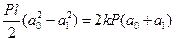
звідки:
 (15)
(15)
Для 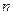 повних коливань
повних коливань
 (16)
(16)
Підставивши в цей вираз  та
та 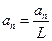 одержимо робочу формулу
одержимо робочу формулу
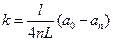 (17)
(17)
Дата добавления: 2015-09-11; просмотров: 1570;
