Лабораторна робота 126. Дослідження коливної системи з двома ступенями вільності
Завдання: дослідити особливості коливань двох однакових фізичних маятників зв’язаних пружиною.
Приладдя: лабораторна установка, секундомір, транспортир, набір пружин.
Теоретичний матеріал : гармонічні коливання, їхнє рівняння та розв’язок; амплітуда, частота, фаза, додавання гармонічних коливань одного напряму; биття; фізичний маятник; загасаючі і вимушені коливання.
Література:
1. Р.10. §§. 10.1 - 10.11;
2. Р.8. §.§. 8.1 – 8.14;
3. §§. 15.1 – 15.12;
4. §§. 63 - 70;
5. §§. 50 - 55.
Опис установки : схема лабораторної установки подана на рис.1. Установка складається з двох однакових маятників, зв’язаних пружиною 2, жорсткість якої k. Для вимірювання періодів коливань використано секундомір з фотоелектричним датчиком.
Виведення робочих формул.Розглянемо коливну систему, що має два степені вільності, між якими може здійснюватись перерозподіл енергії. Кути відхилення обох маятників від положення рівноваги будемо вважати додатними у разі зміщення маятників від вертикального положення проти руху годинникової стрілки. Кожний маятник бере участь в періодичному обертовому русі й може бути описаний рівнянням обертового руху тіла. Моменти сил, що діють на маятник матимуть вигляд
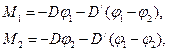 (1)
(1)
де D – коефіцієнт, що визначається масою і геометрією самого маятника, а 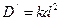 , де k – коефіцієнт жорсткості пружини, d – віддаль від точки підвісу маятника до місця кріплення пружини. Рівняння руху маятників
, де k – коефіцієнт жорсткості пружини, d – віддаль від точки підвісу маятника до місця кріплення пружини. Рівняння руху маятників
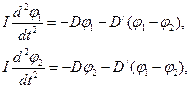 (2)
(2)
де I – момент інерції кожного маятника.
Додаючи і віднімаючи рівняння (2), отримуємо
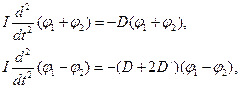 (3)
(3)
Кожне з рівнянь (3) описує гармонічні коливання з частотами 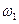 і
і 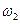 або, відповідно, з періодами
або, відповідно, з періодами 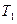 і
і 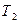 :
:
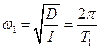 ,
, 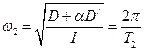 (4)
(4)
Розв’язки рівнянь (3) мають вигляд
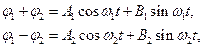 (5)
(5)
Меншу з частот (4) називають основною частотою, а коливання, що мають цю частоту – основними. З частотою 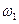 коливається кожний з маятників, якщо позбутися зв’язку між ними. Коефіцієнти
коливається кожний з маятників, якщо позбутися зв’язку між ними. Коефіцієнти 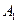 ,
, 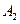 ,
, 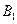 ,
, 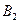 визначають з початкових умов коливань системи.
визначають з початкових умов коливань системи.
Розглянемо частинні випадки.
Синфазні коливання.
Задамо початкові умови в такому вигляді: в момент часу t=0
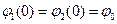 і
і 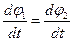 (6)
(6)
Підставивши (6) в (5), отримуємо
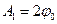 ,
, 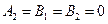 і
і
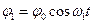
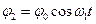 (7)
(7)
Роль зв’язку у разі такого коливання зникає і маятники коливаються синфазно з основною частотою 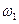 (рис. 2б).
(рис. 2б).
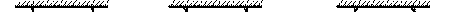
Зустрічні коливання.
Нехай тепер 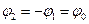 при t=0 і
при t=0 і 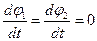 .
.
З (5) маємо
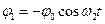
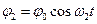 . (8)
. (8)
Маятник здійснює дзеркально-симетричні коливання однакової частоти 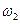 (рис.2.в). Наявність зв’язку між маятниками тут вже дуже суттєва.
(рис.2.в). Наявність зв’язку між маятниками тут вже дуже суттєва.
Биття.
Розглянемо початкові умови : 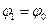 ,
, 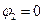 при t=0 і
при t=0 і 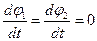 . Коефіцієнти в (5) мають вигляд
. Коефіцієнти в (5) мають вигляд 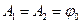 ,
, 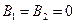 , і
, і
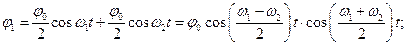 (9)
(9)
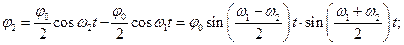 (10)
(10)
Рівняння руху маятників (9) і (10) можна інтерпретувати наступним чином. У разі слабкого зв’язку між маятниками (мале 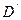 )
) 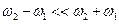 і рівняння руху можна переписати у вигляді
і рівняння руху можна переписати у вигляді
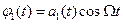 ;
; 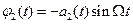 , (11)
, (11)
де 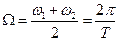 ;
; 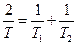 (12)
(12)
Функції 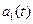 і
і 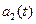 можна розглядати як амплітуди першого і другого коливань, які повільно змінюються з часом порівняно з
можна розглядати як амплітуди першого і другого коливань, які повільно змінюються з часом порівняно з 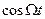 і
і 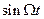 , відповідно. Такий вид коливань називається биттями, а час
, відповідно. Такий вид коливань називається биттями, а час 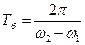 - періодом биття. На рис.3. зображені графіки функцій
- періодом биття. На рис.3. зображені графіки функцій 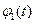 і
і 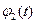 . Фази коливань маятників відрізняються на
. Фази коливань маятників відрізняються на 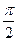 . Під час зменшення амплітуди одного маятника амплітуда другого збільшується. Загальна енергія системи (без врахування втрат) залишається постійною, але весь час переходить від одного маятника до іншого. Між величинами
. Під час зменшення амплітуди одного маятника амплітуда другого збільшується. Загальна енергія системи (без врахування втрат) залишається постійною, але весь час переходить від одного маятника до іншого. Між величинами 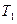 ,
, 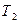 , і
, і 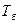 існує просте співвідношення
існує просте співвідношення
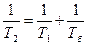 (13)
(13)
Введемо коефіцієнт зв’язку між маятниками
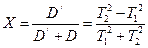 (14)
(14)

Тоді X=0 при відсутності зв’язку ( 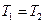 ) і X=1 при жорсткому зв’язку. В загальному випадку коефіцієнт зв’язку змінюється між нулем і одиницею (
) і X=1 при жорсткому зв’язку. В загальному випадку коефіцієнт зв’язку змінюється між нулем і одиницею ( 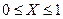 ) в залежності від жорсткості пружини k.
) в залежності від жорсткості пружини k.
Дата добавления: 2015-09-11; просмотров: 786;
