Интерполирование с кратными узлами
Задача, в которой параметры интерполирования – коэффициенты интерполяционного многочлена – определяются только значениями интерполируемой функции, называют задачей интерполирования по Лагранжу, а сам процесс построения интерполяционного полинома – процессом Лагранжа.
Рассмотрим теперь более широкую задачу – задачу интерполирования по значениям функции и ее производных , или задачу кратного интерполирования.
Пусть на сетке 
в узлах 
заданы значения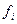 
некоторой функции f и ее производные
,
причем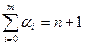 
требуется построить многочлен 
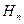, значения которого и производные до порядка 
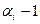в узлах 
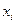(i=0,1,…,m) совпадают со значениями 
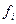и соответствующими ее производными, а также оценить погрешность.
Такой вид интерполирования называют интерполированием по Эрмиту, а соответствующий многочлен 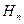- многочленом Эрмита. Числа 
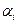называют кратностями узлов 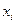. При этом можно доказать, что многочлен Эрмита существует и единственен.
.
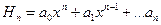Остаточный член интерполяционной формулы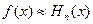 
…. можно представить в следующем виде:
.
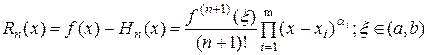. (4.44)
Пусть для определенности
. (4.45)
Используя это ограничение и формулу (4.44), получим оценку погрешности для фиксированной точки x:
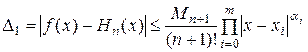. (4.46)
Построение равномерной на всем отрезке [a,b] оценки для фиксированной сетки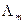 
теперь не представляет труда. Действительно,
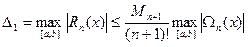, (4.47)
где
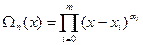. (4.48)
Пример 4.4. Построить интерполяционный многочлен Эрмита для функции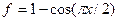 
по узлам 
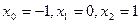соответственно с кратностями 
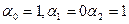. Получить равномерную оценку погрешности на отрезке [-1,1].
Вычислим в заданных узлах значение функции и ее производной:
; 
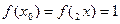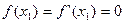
Построим многочлен Эрмита с учетом кратностей узлов:
.
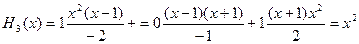Найдем оценку погрешностей. Используя формулу (4.47) и учитывая, что для рассматриваемой функции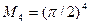 
, получим
.
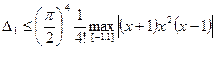Нетрудно показать, что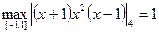 
. Поэтому окончательно имеем 
.
Дата добавления: 2015-11-06; просмотров: 1478;