Закон распределения модуля разности
Если две случайные величины x1 и х2 каждая в отдельности имеют нормальное распределение с параметрами  и
и 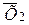 и
и 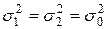 , то модуль разности этих величин
, то модуль разности этих величин
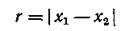
имеет распределение, которое носит название закона распределения модуля разности. Этому закону распределения, например, часто подчиняются погрешности взаимно расположенных поверхностей и осей, а также погрешности формы деталей: овальность, конусность.
Плотность вероятности или дифференциальная функция распределения случайной величины r выражается следующим уравнением:
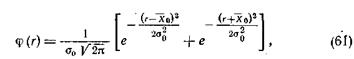
где 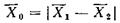 и s0 являются параметрами распределения модуля разности r.
и s0 являются параметрами распределения модуля разности r.
Интегральная функция распределения модуля разности r выражается следующим уравнением:
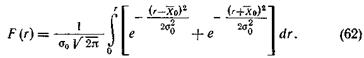
Произведя замену переменных в уравнениях (61) и (62):
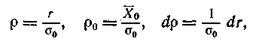
получим следующие выражения:
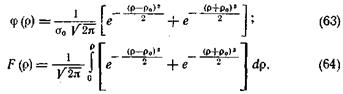
Вид кривой распределения j(р) зависит от значения r0. При r0 = 0 кривая резко асимметрична, при r0 = 3 она совпадает с кривой нормального распределения (рис. 20).
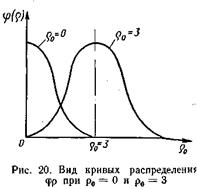 Если обозначить r - r0 = t1, а r + r0 = t2, то уравнение (64) можно заменить следующим уравнением:
Если обозначить r - r0 = t1, а r + r0 = t2, то уравнение (64) можно заменить следующим уравнением:
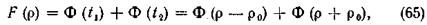
так как каждое слагаемое уравнения (64) является функцией Лапласа 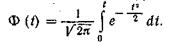
Дата добавления: 2015-10-05; просмотров: 2463;
