Закон равной вероятности

Закон распределения случайной величины непрерывного типа обычно задается либо с помощью плотности вероятности j(х), либо с помощью функции распределения F(х). Если непрерывная случайная величина х при испытаниях принимает все значения интервала (а — b) с одинаковой плотностью вероятности, то распределение плотности вероятности графически будет выражаться в виде прямоугольника с основанием ab и высотой j (х) = const (рис. 16).

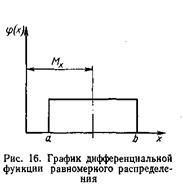Такой закон распределения непрерывной случайной величины называется законом равной вероятности, а само распределение— равномерным.

При интервале изменений случайной величины х от а до b:

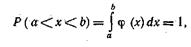
т. е. вероятность того, что случайная величина х при испытаниях будет принимать значения в интервале от а до b, равна площади под дифференциальной кривой распределения. В соответствии с рис. 16 эта площадь представляет собой прямоугольник с основанием ab и высотой j (х), следовательно,

Отсюда уравнение дифференциальной функции распределения или плотности вероятности будет иметь следующий вид:

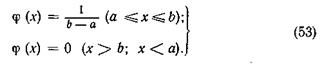
Закон равной вероятности имеет два параметра: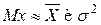

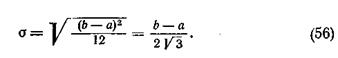
Интегральная функция равномерного распределения выражается следующим уравнением для (а < х < b):

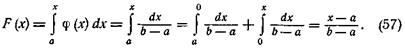
Если х < а, то F(х) = 0; если х ³ b, то F(х) = 1. Когда а = - b, Мх = 0, то 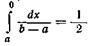и для этого случая уравнение (57) примет вид