Характеристики уклонений от нормального закона

Закон нормального распределения является симметричным относительно ординаты точки х = 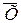. Однако на практике встречаются кривые распределения, уклоняющиеся от нормального распределения. Они могут быть асимметричными, когда 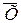не совпадает с Мо, или иметь большую или меньшую крутизну, когда вершина кривой распределения является более острой или более плоской по сравнению с теоретической кривой нормального распределения (рис. 15).

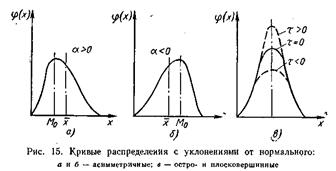Для оценки уклонений распределения от нормального пользуются двумя безразмерными характеристиками: коэффициентом асимметрии a и коэффициентом крутости или эксцессом t. Асимметрия считается положительной, если Мо лежит влево от ординаты 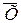, и отрицательной, когда она лежит справа от .

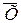Мера асимметрии вычисляется по формуле

где п — объем совокупности.

Если a > 0, то асимметрия положительная; при a < 0 — асимметрия отрицательная; при a = 0 — асимметрия отсутствует.

Мера крутости (эксцесс) распределения вычисляется по формуле

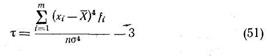
Если t > 0, то вершина кривой выше нормальной, эксцесс положительный; если t < 0, вершина ниже нормальной, эксцесс отрицательный; при t = 0 эксцесс отсутствует, кривая нормальная.