Закон биномиального распределения
Пусть производится серия последовательных независимых испытаний, каждое из которых заканчивается одним из двух несовместимых между собой результатов: или событие А наступает, или оно не наступает. Вероятность появления события А в каждом испытании равна р, а вероятность непоявления события А равна q = 1 - р. Так как испытания независимы то вероятность появления или непоявления события А не зависит от результатов предыдущих испытаний. При такой схеме испытаний вероятность появления события А заданное число раз подчиняется закону биномиального распределения, который можно сформулировать так: если вероятность события А постоянна в серии последовательных независимых испытаний и равна р, то вероятность появления события А ровно k раз в n испытаниях будет равна

Это уравнение определяет собой распределение вероятностей случайного числа k, которое называется биномиальным.
В формуле (36) символ 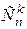 обозначает число сочетаний из n элементов по k, т. е. биномиальный коэффициент. Биномиальный коэффициент можно проще записать так:
обозначает число сочетаний из n элементов по k, т. е. биномиальный коэффициент. Биномиальный коэффициент можно проще записать так:
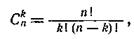
где символ n! обозначает факториал и выражает произведение натуральных чисел 1, 2, 3, …, n. При этом 0! = 1. С учетом изложенного формула (36) примет более простой вид:
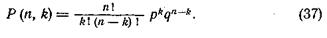
Математическое ожидание Mk и дисперсия 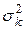 биномиального распределения равны:
биномиального распределения равны: 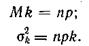
Дата добавления: 2015-10-05; просмотров: 694;
