Случайные величины и их распределение
Случайные величины подразделяются на дискретные и непрерывные.
Дискретными случайными величинами называются такие, которые в результате испытаний могут принимать лишь отдельные, изолированные, большей частью целочисленные значения, и не могут принимать значения, промежуточные между ними.
Непрерывной случайной величиной называется такая, которая в результате испытаний может принимать любые численные значения из непрерывного ряда их возможных значений в границах определенного интервала.
Возможности случайных величин принимать при испытаниях те или иные численные значения оцениваются при помощи вероятностей. Совокупность значений случайных величин, расположенных в возрастающем порядке с указанием их вероятностей, называется распределением случайных величин. Различают теоретические и эмпирические распределения случайных величин. В теоретических распределениях оценка возможных значений случайной величины производится при помощи вероятностей, а в эмпирических — при помощи частот или частостей, полученных в результате опытов или испытаний.
Распределения случайных величин дискретного типа можно представить в виде табл. 1 и 2 или графика (рис. 1), составленного на основании табл. 2.
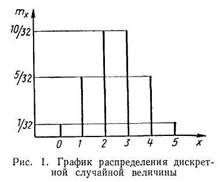


На практике при изучении случайных величин непрерывного типа полученные значения их разбивают на интервалы или разряды с таким расчетом, чтобы величина разряда была несколько больше цены деления шкалы измерительного инструмента и таким образом компенсировалась бы погрешность измерений. 






Эмпирическое распределение случайной величины непрерывного типа (см. табл. 3) может быть представлено в виде ступенчатого графика или в виде ломаной кривой (рис. 2). Ступенчатый график называется гистограммой распределения, а ломаная кривая — полигоном распределения или эмпирической кривой распределения.
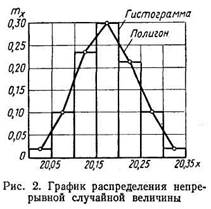 При теоретических описаниях и изучениях случайных величин непрерывного типа затруднительно производить разбивку их на разряды. Поэтому во избежание этих затруднений вводится понятие функции распределения.
При теоретических описаниях и изучениях случайных величин непрерывного типа затруднительно производить разбивку их на разряды. Поэтому во избежание этих затруднений вводится понятие функции распределения.
Пусть X — случайная величина, а х — какое-либо действительное число: при этом X < х и этому событию отвечает вероятность Р(X < х), которая, очевидно, является функцией х, т. е. P(X<x) = F(x),
F(x) называется функцией распределения вероятностей случайной величины или интегральной функцией распределения.
Для непрерывной случайной величины график интегральной функции распределения будет иметь вид не ступенчатой, а монотонно возрастающей кривой, имеющей касательную к каждой точке (рис. 4).
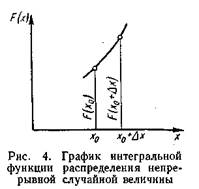 Интегральная функция распределения непрерывной случайной величины является дифференцируемой функцией. Первая производная от интегральной функции называется дифференциальной функцией распределения, или плотностью вероятности. Будем обозначать ее через j(x). Исходя из определения производной, можно, написать
Интегральная функция распределения непрерывной случайной величины является дифференцируемой функцией. Первая производная от интегральной функции называется дифференциальной функцией распределения, или плотностью вероятности. Будем обозначать ее через j(x). Исходя из определения производной, можно, написать
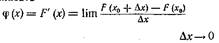
или, учитывая равенство (1),
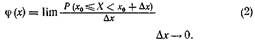
Дата добавления: 2015-10-05; просмотров: 890;
