Случайное событие, случайная величина и вероятность
В теории вероятностей и основанной на ней математической статистике приходится встречаться с рядом специфических понятий, из которых основными являются следующие: испытание, событие, случайная величина, вероятность, частота и частость.
Испытанием называется практическое осуществление какого-либо комплекса условий.
Событием называется явление, происходящее в результате осуществления определенного комплекса условий, т. е. в результате испытания.
Явления или события, происходящие при многократном повторении испытаний, называются массовыми. Если при каждом испытании неизбежно происходит событие А, то такое событие называется достоверным. Если в условиях данного испытания некоторое событие В заведомо не может произойти, то оно называется невозможным. Если же при испытаниях может произойти либо событие А, либо В, либо С и т. д., то такие события называются возможными или случайными. Следовательно, случайным называется такое событие, которое при испытании может либо наступить, либо не наступить.
Теория вероятностей имеет дело не только со случайными событиями, но также и со случайными величинами. Случайной величиной называется переменная величина, которая в результате испытаний может принять то или иное значение в границах определенного интервала.
Любое случайное событие обладает той или иной объективной возможностью или необходимостью своего проявления. Для количественной оценки возможности осуществления случайного события пользуются термином вероятность. Вероятность какого-либо события А обозначается символом Р(А) (от слова probabilitas — вероятность) и представляет собой численную меру объективной возможности этого события.
Для сравнения между собой различных событий по степени возможности их осуществления необходимо установить какую-то единицу измерения. В качестве такой единицы измерения принята вероятность достоверного события. Вероятность достоверного события принимается равной единице. Вероятность всех других событий — возможных, но не достоверных — будет характеризоваться числами, меньшими единицы, а вероятность невозможного события будет равна нулю.
Существуют классическое и статистическое определение этого понятия. По классическому определению вероятностью события А называется отношение числа случаев m, благоприятствующих этому событию, к числу n всех возможных случаев данного класса испытаний, т. е.
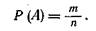
При этом число всех случаев n должно быть конечно и все они должны быть равновозможны, несовместимы и независимы.
Под несовместимыми понимаются такие события, которые не могут появляться вместе, одновременно; под независимыми событиями понимаются такие, появление которых не зависит от того, какое событие произошло перед этим; под данным классом испытаний подразумевается совокупность неизменных условий, осуществление которых приводит к тому или иному событию.
При изучении массовых явлений какое-либо случайное событие или случайная величина могут появляться несколько раз в процессе испытаний. Например, пусть при N испытаниях событие А фактически появилось f раз. Число f носит название частоты появления события А. Отношение частоты события А к общему числу испытаний N носит название частости события или относительной частоты, которую будем обозначать mА:
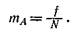
Дата добавления: 2015-10-05; просмотров: 1124;
