Закон редких событий (Пуассона)

Если вероятность р события А очень мала (p£ 0,1), а число испытаний велико, то вероятность того, что событие А наступит k раз в n испытаниях, будет равна

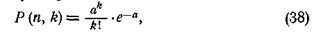
где а = nр = Mk — математическое ожидание числа k.

Уравнение (38) определяет собой распределение редких событий, или распределение Пуассона.

Когда число испытаний n велико, а р мало, то закон биномиального распределения и закон редких событий практически совпадают. Это имеет место тогда, когда р £ 0,1 и рn< 4. При этих условиях вместо формулы (37) можно применить формулу (38), т. е.

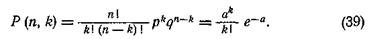
Принимая во внимание, что а = nр, формула (39) примет вид

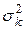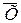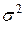Распределение Пуассона имеет только один параметр а = nр = Mk. Для этого распределения дисперсия численно равна математическому ожиданию: = Mk. Поэтому, когда в распределении дискретной случайной величины и мало отличаются друг от друга по своим численным значениям, то можно уверенно считать, что данное распределение подчиняется закону редких событий.

Закон редких событий имеет практическое применение в машиностроении для выборочного контроля готовой продукции, когда по техническим условиям в принимаемой партии продукции допускается некоторый процент брака (обычно небольшой) и поэтому всегда р << 0,1, а объем выборки n берут таким, чтобы было пр < 4.