Закон распределения эксцентриситета (Релея)

Закон распределения эксцентриситета, или закон Релея, имеет место при отклонениях эксцентриситета осей или биении поверхностей деталей, которые являются непрерывными случайными величинами. Этот закон однопараметрический и дифференциальная функция распределения его имеет выражение:

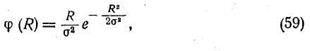
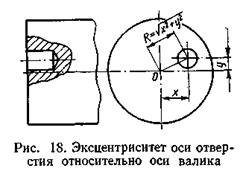
где R — переменная величина эксцентриситета или биения, причем , а х и у — координаты точки конца R (рис. 18);

s — среднее квадратическое отклонение значений координат х и у, имеющих одинаковое распределение; поэтому s = s_x = s_y.

Интегральный закон распределения эксцентриситета имеет выражение

Графическое изображение дифференциального закона распределения эксцентриситета дано на рис. 19.

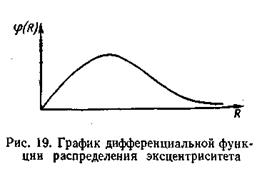
Особенностью данного распределения является, то что в основе его лежит нормальное распределение, так как координаты х и у точки конца R распределены нормально, а само распределение R не является нормальным. Связь между s_R, R и s выражается следующими зависимостями:

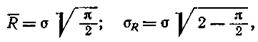
где - среднее значение (математическое ожидание) случайной величины R; s_R — среднее квадратическое отклонение R от .