Конечные разности
Пусть дана функция 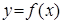 и фиксированная величина приращения аргумента
и фиксированная величина приращения аргумента 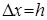 . Конечной разностью первого порядка функции y называется выражение.
. Конечной разностью первого порядка функции y называется выражение. 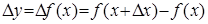 Конечной разностью второго порядка называется:
Конечной разностью второго порядка называется: 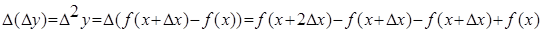 . Kонечной разностью n-го порядка называется
. Kонечной разностью n-го порядка называется 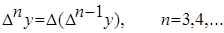 . Конечные разности обладают следующими свойствами :
. Конечные разности обладают следующими свойствами :
1. 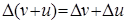 ;
;
2. 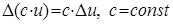 ;
;
3. 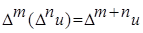 .
.
Для малых h можно приближенно заменять производные через конечные разности: 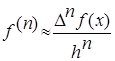 , (
, ( 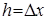 ).
).
Часто приходится рассматривать функции у=f(x), заданные табличными значениями yi=f(xi), для системы равноотстоящих точек xi(i=0,1,2,…), где
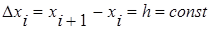 . Конечные разности последовательности yiопределяются соотношениями
. Конечные разности последовательности yiопределяются соотношениями
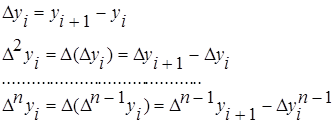
Пример 5.1 Построить конечные разности для функции 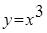 с шагом
с шагом 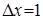 .
.
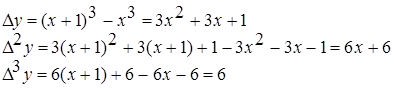
Конечные разности различных порядков удобно располагать в форме таблиц двух видов: горизонтальной (таблица 5.1) или диагональной (таблица 5.2)
Таблица 5.1.
Горизонтальная таблица разностей
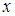
| 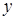
| 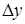
| 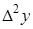
| 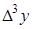
| 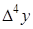
|
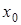
| 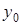
| 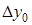
| 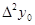
| 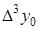
| 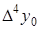
|
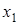
| 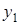
| 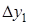
| 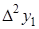
| 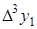
| |
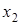
| 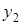
| 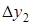
| 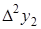
| ||
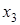
| 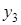
| 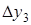
| |||
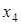
| 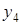
| ||||
| …. | … | … | … | … | … |
Таблица 5.2.
Диагональная таблица конечных разностей
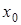
| 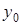
| 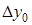
| 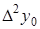
| 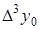
|
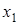
| 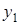
| |||
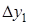
| ||||
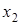
| 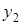
| 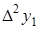
| ||
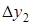
| ||||
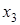
| 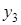
|
Дата добавления: 2015-10-09; просмотров: 798;
