Интерполяционная формула Ньютона №1
Пусть точки xi будут равноотстоящими. Дано: отрезок 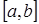 ,
, 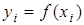 ,
, 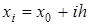 .
.
Тогда: 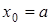 ,
, 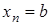 ,
, 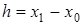 - шаг интерполяции.
- шаг интерполяции.
Требуется: подобрать полином 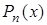 , степени не выше n, принимаю-щий в точках значения
, степени не выше n, принимаю-щий в точках значения 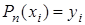 или
или 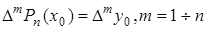 .
.
Ньютон находил решение в виде полинома 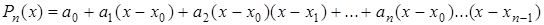 ,
,
где 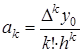 .
.
Для практического использования удобно положить 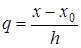 , тогда
, тогда 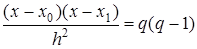 . …
. … 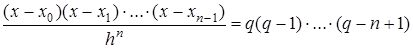
Получим:
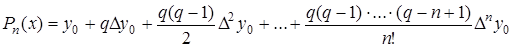
- первый многочлен Ньютона.
Полученную формулу выгодно использовать для интерполирования функции 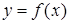 в окрестности начального значения x0, где q мало по абсолютной величине.
в окрестности начального значения x0, где q мало по абсолютной величине.
При n=1 получим формулу линейного интерполирования
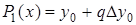
Остаточный член 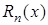 первой интерполирующей формулы Ньютона имеет вид:
первой интерполирующей формулы Ньютона имеет вид:
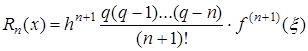 ,
,
где 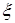 - некоторая внутренняя точка наименьшего промежутка, содержащего все узлы
- некоторая внутренняя точка наименьшего промежутка, содержащего все узлы 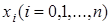 и точку
и точку 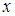 .
.
При наличии дополнительного узла 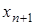 на практике пользуются более удобной приближенной формулой:
на практике пользуются более удобной приближенной формулой:
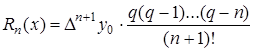 .
.
Дата добавления: 2015-10-09; просмотров: 748;
