Метод математической индукции

1. Натуральные числа.Логическое обоснование понятия натурального числа было дано в XIX веке в работах итальянского математика и логика Пеано (1858 – 1932 гг.). Как и во всякой аксиоматической теории, в теории Пеано дается перечень первоначальных понятий (объектов и отношений) и перечень аксиом.

Первоначальные объекты: множество N, элементы которого называются натуральными числами, и выделенный в этом множестве элемент 1, называемый единицей.

Первоначальное понятие – отношение «следует за» на множестве N. Через 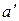будем обозначать элемент, который следует за элементом а.

Аксиомы:

1) Существует натуральное число 1 (единица), которое не следует ни за каким натуральным числом, т.е. .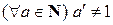

2) Для любого натурального числа 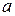существует следующее за ним натуральное число 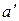, и притом только одно, т.е. .

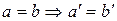3) Каждое натуральное число следует не более чем за одним натуральным числом, т.е. .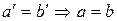

4) (Аксиома индукции). Любое подмножество 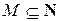, обладающее свойствами:

а) ;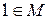

б) ;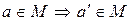

совпадает с множеством N всех натуральных чисел.

Опираясь только на эти аксиомы и определив операции сложения и умножения, можно построить всю арифметику натуральных чисел. В частности, можно на множестве N определить порядок «меньше» и доказать, что всякое подмножество из N имеет наименьший элемент. Эта работа будет проделана позже в дисциплине «Числовые системы». Здесь аксиоматика Пеано приводится лишь для того, чтобы подчеркнуть, что принцип индукции, который широко применяется в математике, по существу является лишь другой формой аксиомы 4).

2. Индукция и дедукция.Рассматриваемые в математике утверждения можно условно разбить на общие и частные.

Например:

1) ;

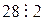2) Всякое число, оканчивающееся четной цифрой, делится на 2.

Здесь утверждение 1) есть частный случай утверждения 2).

Дедукция – это метод рассуждения (доказательства) от общего к частному. Аксиоматический метод – это тоже дедуктивный метод. Примером дедукции является также использование общих теорем при решении конкретных задач.

Индукция – это метод рассуждения от частного к общему, т.е. рассуждения, при которых общий вывод делается при изучении частных фактов.

Если общий вывод делается на основании изучения всех частных случаев, то индукция называется полной. Если же вывод делается на основании изучения только части всех частных случаев, то индукция называется неполной. Неполная индукция широко применяется в экспериментальных науках и в математике для создания научных гипотез. Однако в математике неполная индукция доказательной силы не имеет. Так, изучая арифметическую прогрессию 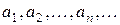, мы замечаем, что 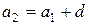, , 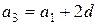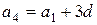. Эти частные случаи наводят нас на мысль, что при любом n

.

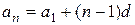Как известно, эта догадка действительно верна.

Другой яркий пример. Более трехсот лет назад французский математик Пьер Ферма (1608–1665) высказал предположение, что при любом натуральном 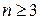уравнение 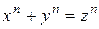не имеет решений в натуральных числах (великая теорема Ферма). Долгое время попытки многих математиков и нематематиков доказать или опровергнуть это предположение были безуспешными (подробная история изложена, например, в популярной книге М.М.Постникова. Теорема Ферма. - М.: Наука, 1978). И лишь сравнительно недавно в 1993 г. профессор Принстонского университета Эндрю Уайлс доказал (как это сейчас уже признано специалистами) справедливость этой теоремы.

Однако неполная индукция может привести к неверному выводу. Так Л.Эйлер указал многочлен 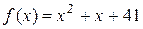, который в качестве значений для чисел от 0 до 39 дает простые числа: 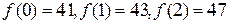и т.д. Однако 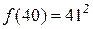. Другой яркий пример. Еще П.Ферма (1601–1665) заметил, что числа 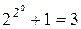, , 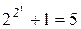, , 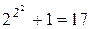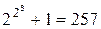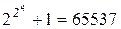простые и естественно предположил, что все числа вида 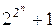– простые. Однако Эйлер показал, что уже число 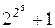делится на 641, и тем самым опроверг предположение Ферма. Таким образом, неполная индукция действительно не имеет доказательной силы. Ниже мы сформулируем так называемый принцип математической индукции в нескольких формах, который позволяет обосновывать утверждения, зависящие от натурального числа n и справедливые для любого n или почти для всех натуральных чисел.