Принцип математической индукции.

Т е о р е м а 1(обычный принцип математической индукции).Если для предиката 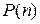, определенного на множестве N, выполнены следующие два условия:

1) предикат 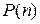истинен при 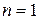, т. е. высказывание 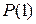истинно;

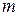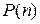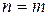2) для любого натурального из истинности предиката при следует его истинность при 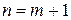, т. е. ;

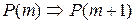то предикат P(n) является истинным при любом натуральном 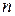, т.е. в 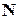истинно высказывание .

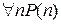□ Обозначим через M множество всех натуральных чисел n, для которых предикат 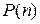истинен, т.е.

.

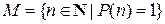Тогда из условия теоремы 1 вытекает, что

1) 1 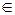M;

2) .

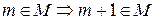Таким образом, оба условия аксиомы индукции выполнены и поэтому M=N, т.е. предикат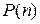истинен при любом натуральномn.

Схема доказательства обычным методом математической индукции:

База индукции.Устанавливают истинность предиката 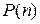при .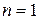

Шаг индукции.Предположив истинность предиката 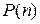при 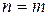,доказывают его истинность при .

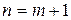Вывод.На основании обычного принципа математической индукции истинно высказывание .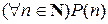

Пример 1.Доказать, что для любого натурального n справедливо равенство

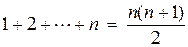. (1)

□ Применим обычный принцип математической индукции.

База индукции. При 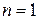равенство (1) истинно, так как его левая и правая части равны 1.

Шаг индукции. Пусть (1) справедливо для 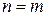, т.е.

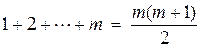. (2)

Рассмотрев левую часть (1) при 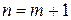, преобразовав ее и воспользовавшись предположением индукции (2), получим

=

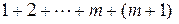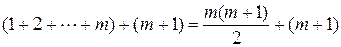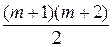= = . (3)

Равенство (3) означает истинность формулы (1) при .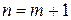

Вывод. Равенство (1) справедливо при любом натуральном n .

Иногда предикат 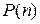неимеет смысла при 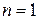, а имеет смысл для натуральных чисел, начиная с некоторого натурального числа 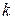. В некоторых случаях предикат имеет смысл для любых неотрицательных целых чисел. Чтобы сформулировать принцип математической индукции, охватывающий все эти случаи, введем следующие два обозначения:

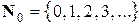– множество всех неотрицательных целых чисел;

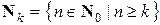– множество всех неотрицательных целых чисел, больших или равных k (k = 0, 1, 2, …).

Т е о р е м а 2(обобщенный принцип математической индукции).Если предикат P(n) определен на множестве 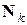и выполнены следующие два условия:

1) высказывание 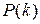истинно;

2) для любого натурального 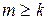из истинности 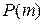следует истинность 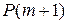, т. е. ;

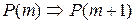то предикат P(n) является истинным при любом натуральном 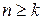, т. е. истинно высказывание .

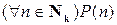□ Введем в рассмотрение новый предикат 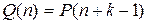. Для предиката выполненыусловия1) и 2) теоремы 1 и поэтому он истинен при любом натуральном 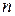. Но тогда предикат 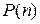истиненприлюбом .

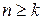Заметим, что частным случаем этого принципа при 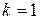является обычный принцип математической индукции. В отдельных случаях удобно применять этот принцип и при .

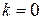Т е о р е м а 3(Обобщенный усиленный принцип математической индукции).Если предикат 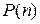определен на множестве 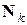и выполнены следующие два условия:

1) высказывание 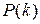истинно;

2) для любого натурального 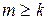из истинности 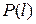для любого натурального 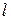такого, что 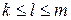, следует истинность ;

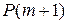то предикат P(n) является истинным при любом натуральном 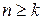, т. е. истинно высказывание .

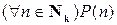□ Пусть выполнены условия теоремы 3 и предположим, что существует такое натуральное число 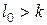, что P(l₀) – ложное высказывание. Пусть

.

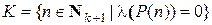Множество 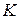не пусто, так как 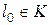. Пусть 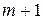– наименьший элемент множества 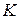, в частности, 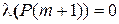. Тогда для любого натурального 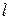такого, что 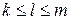, высказывание 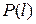истинно. В силу условия 2) теоремы 3 высказывание 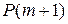тоже обязано быть истинным, вопреки выбору числа 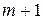. Таким образом, предикат 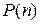является истинным при любом натуральном .

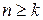Замечание 1.При 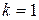имеем 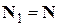и последний принцип называют усиленным принципом математической индукции.

Перечисленные принципы позволяют указать следующую общую схему доказательства методом математической индукции:

База индукции.Устанавливают истинность предиката .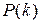

Шаг индукции.Предположив истинность утверждения 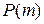при 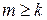( 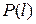при любом натуральном 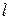таком, что 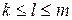, в случае усиленного принципа) доказывают истинность утверждения 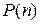при .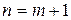

Вывод.На основании обобщенного принципа (усиленного принципа) математической индукции высказывание 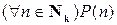истинно.

Пример 2.Доказать, что любую сумму 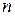рублей, большую 3, можно выплатить монетами достоинством в 2 и 5 рублей.

□ Переведем условие задачи на математический язык, т.е., как говорят, составим математическую модель задачи. Легко понять, что решение задачи равносильно доказательству истинности того, что уравнение

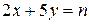(4)

имеет решение в неотрицательных целых числах при любом 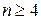. Что, в свою очередь, эквивалентно доказательству истинности предиката 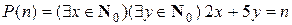во множестве 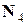. Применим обобщенный принцип индукции.

База индукции.При 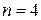имеем 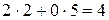, т.е. пара 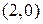есть решение уравнения (4) при 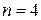и высказывание 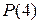истинно.

Шаг индукции.Предположим истинность высказывани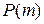я для 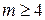, т.е. справедливость равенства

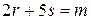(5)

для некоторых неотрицательных целых чисел 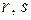. Прибавляя к обеим частям равенства (5) число 1, получим равенство

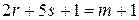. (6)

Проанализируем последнее равенство. Если 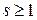, то, переписывая равенство (6) в виде

,

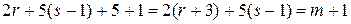получаем, что пара 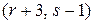неотрицательных целых чисел является решением уравнения (4) при 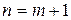. Если 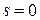, то из того, что 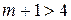, с неизбежностью следует неравенство 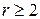. Переписывая равенство (6) в виде

,

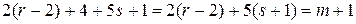заключаем, что пара 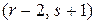неотрицательных целых чисел является решением уравнения (4) при .

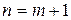Вывод.На основании обобщенного принципа математической индукции при 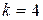делаем вывод, что высказывание 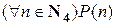истинно.

В дальнейшем у нас будет возможность проиллюстрировать метод математической индукции при доказательстве других утверждений.