Теоремы и их доказательство
Обычно теоремы имеют вид либо импликации  , либо эквиваленции
, либо эквиваленции 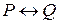 , где
, где 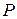 и
и 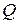 – некоторые предикаты. Основной целью этого параграфа является указание основных методов доказательства таких теорем. Заметим, что мы, следуя традиции, употребляем привычную фразу «доказательство теоремы»; точнее было бы говорить не о доказательстве теоремы, а доказательстве того, что соответствующие предикаты
– некоторые предикаты. Основной целью этого параграфа является указание основных методов доказательства таких теорем. Заметим, что мы, следуя традиции, употребляем привычную фразу «доказательство теоремы»; точнее было бы говорить не о доказательстве теоремы, а доказательстве того, что соответствующие предикаты  и
и 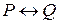 является тождественно истинными, т.е. являются теоремами.
является тождественно истинными, т.е. являются теоремами.
1. Теоремы вида  . Наиболее часто встречаются теоремы вида
. Наиболее часто встречаются теоремы вида  (если
(если 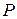 , то
, то 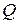 ), в которой
), в которой 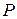 называют условием, а
называют условием, а 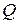 – заключением теоремы
– заключением теоремы  . Доказать такую теорему – значит установить истинность импликации
. Доказать такую теорему – значит установить истинность импликации  . Так как импликация всегда истинна при ложной посылке
. Так как импликация всегда истинна при ложной посылке 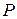 , то достаточно из истинности
, то достаточно из истинности 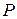 вывести истинность
вывести истинность 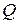 , т.е. показать, что из
, т.е. показать, что из 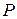 логически следует
логически следует 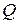 . Укажем некоторые схемы доказательства теорем вида
. Укажем некоторые схемы доказательства теорем вида  .
.
1. С помощью цепочки истинных импликаций.
Свойство транзитивности импликации (см. § 2 гл. II) означает, что из истинности формулы  обязательно вытекает истинность импликация
обязательно вытекает истинность импликация 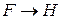 . Таким образом, для доказательства истинности импликации
. Таким образом, для доказательства истинности импликации 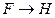 достаточно установить истинность цепочки промежуточных импликаций
достаточно установить истинность цепочки промежуточных импликаций 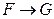 и
и 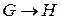 . Этот факт можно распространить на любое число промежуточных импликаций: из истинности импликаций
. Этот факт можно распространить на любое число промежуточных импликаций: из истинности импликаций 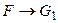 ,
, 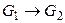 , …,
, …, 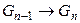 ,
, 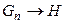 следует истинность импликации
следует истинность импликации 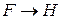 . Таким образом, для доказательства истинности теоремы
. Таким образом, для доказательства истинности теоремы  достаточно установить истинность цепочки промежуточных импликаций
достаточно установить истинность цепочки промежуточных импликаций 
 ,
, 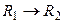 , …,
, …, 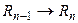 ,
, 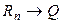 .
.
На самом деле, как уже отмечалось, для доказательства теоремы  достаточно установить, что
достаточно установить, что 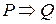 . Учитывая свойство транзитивности отношения следования, основной вывод предыдущего абзаца можно перефразировать в следующем виде: для доказательства истинности теоремы
. Учитывая свойство транзитивности отношения следования, основной вывод предыдущего абзаца можно перефразировать в следующем виде: для доказательства истинности теоремы  достаточно установить следующие логические следования:
достаточно установить следующие логические следования: 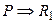 ,
, 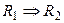 , …,
, …, 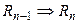 ,
, 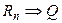 .
.
2. С помощью закона контрапозиции.
С теоремой вида
(1) 
связаны следующие теоремы:
(2)  – обратная теорема по отношению к (1);
– обратная теорема по отношению к (1);
(3) 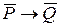 – противоположная теорема по отношению к (1);
– противоположная теорема по отношению к (1);
(4)  – теорема, обратная противоположной теореме.
– теорема, обратная противоположной теореме.
Очевидно, теорема  является обратной по отношению к
является обратной по отношению к  . Таким образом, теоремы (1) и (2) – взаимно обратны. Точно также теоремы (3) и (4) – взаимно обратны.
. Таким образом, теоремы (1) и (2) – взаимно обратны. Точно также теоремы (3) и (4) – взаимно обратны.
Далее, (1) и (3), а также (2) и (4) – взаимно противоположны. Наконец, теоремы (1) и (4), а также (2) и (3) являются обратно противоположными. В силу закона контрапозиции имеем следующие равносильности:
 ,
, 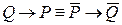 .
.
Таким образом, теоремы, которые между собою обратно противоположны, являются равносильными. Этот закон называется законом контрапозиции.
Таким образом, если доказательство теоремы  сложнее доказательства теоремы
сложнее доказательства теоремы  , то по закону контрапозиции можно доказывать вместо теоремы
, то по закону контрапозиции можно доказывать вместо теоремы  равносильную ей теорему
равносильную ей теорему  , которую называют контрапозитивной по отношению к
, которую называют контрапозитивной по отношению к  . Иногда такое доказательство не совсем точно называют доказательством от противного.
. Иногда такое доказательство не совсем точно называют доказательством от противного.
Пример 1.
(1)  : «Если целое число
: «Если целое число 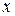 оканчивается нулем, то
оканчивается нулем, то  »;
»;
(2)  : «Если
: «Если  , то
, то 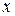 оканчивается нулем»;
оканчивается нулем»;
(3) 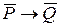 : «Если
: «Если 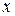 оканчивается не нулем, то
оканчивается не нулем, то 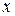 не делится на 5»;
не делится на 5»;
(4)  : «Если
: «Если 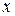 не делится на 5, то
не делится на 5, то 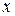 оканчивается не нулем»;
оканчивается не нулем»;
Здесь теоремы (1) и (4) – истинны, а теоремы (2) и (3) – ложны.
Из этого примера видно, что из истинности теоремы  совсем необязательно следует истинность обратной теоремы. Одна из часто встречающихся ошибок в школьной, да и вузовской практике – это отождествления этих теорем. Часто, например, говорят: «Так как
совсем необязательно следует истинность обратной теоремы. Одна из часто встречающихся ошибок в школьной, да и вузовской практике – это отождествления этих теорем. Часто, например, говорят: «Так как  , то по теореме Пифагора треугольник со сторонами 6, 8, 10 – прямоугольный». В действительности это заключение следует не из теоремы Пифагора, а из теоремы, которая обратна теореме Пифагора и которая тоже истинна.
, то по теореме Пифагора треугольник со сторонами 6, 8, 10 – прямоугольный». В действительности это заключение следует не из теоремы Пифагора, а из теоремы, которая обратна теореме Пифагора и которая тоже истинна.
3. Доказательство теорем методом от противного.
Доказательство от противного теоремы  основано на одной из следующих равносильностей:
основано на одной из следующих равносильностей:
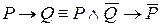 ;
; 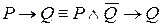 ,
, 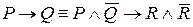
где 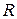 – некоторый вспомогательный предикат. Эти равносильности названы в § 2 гл. II законами доказательства от противного. Таким образом, теорему
– некоторый вспомогательный предикат. Эти равносильности названы в § 2 гл. II законами доказательства от противного. Таким образом, теорему  можно доказать, предположив истинность
можно доказать, предположив истинность 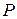 и ложность
и ложность 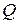 и с помощью логических рассуждений доказать, что выполняется хотя бы одно из следующих трех условий: 1)
и с помощью логических рассуждений доказать, что выполняется хотя бы одно из следующих трех условий: 1) 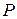 ложно, т.е. получить противоречие с предположением относительно
ложно, т.е. получить противоречие с предположением относительно 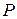 ; 2)
; 2) 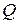 истинно, т.е. получить противоречие с предположением относительно
истинно, т.е. получить противоречие с предположением относительно 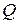 ; 3) доказать одновременную истинность и ложность некоторого вспомогательного высказывания
; 3) доказать одновременную истинность и ложность некоторого вспомогательного высказывания 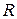 . Этот метод доказательства теорем вида
. Этот метод доказательства теорем вида  называется доказательством от противного.
называется доказательством от противного.
Пример 2. Доказать, что если 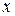 и
и 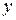 – целые числа,
– целые числа, 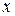 делится на 7 и
делится на 7 и 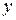 делится на 7, то и сумма
делится на 7, то и сумма 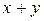 делится на 7.
делится на 7.
□ Соответствующая теорема имеет вид  , где условие
, где условие 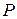 есть предикат
есть предикат 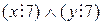 , а заключение
, а заключение 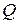 – предикат
– предикат  . Установим тождественную истинность в
. Установим тождественную истинность в 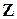 предиката
предиката
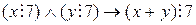
методом от противного.
Предположим противное, т.е. что этот предикат не является тождественно истинным. Это означает, что существуют такие значения переменных 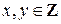 , что высказывание
, что высказывание  ложно, т.е. посылка
ложно, т.е. посылка 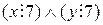 истинна, а заключение
истинна, а заключение 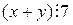 ложно. Имеем
ложно. Имеем 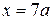 ,
, 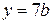 ,
, 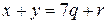 для некоторых
для некоторых 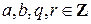 , причем
, причем 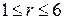 . Выражая
. Выражая 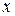 из последнего равенства, получим
из последнего равенства, получим 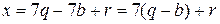 . Отсюда следует, что
. Отсюда следует, что 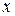 не делится на 7. Получили противоречие:
не делится на 7. Получили противоречие: 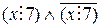 . Доказательство проходило по схеме
. Доказательство проходило по схеме 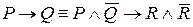 , где
, где 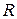 есть предикат
есть предикат 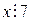 . В силу закона от противного справедлива теорема
. В силу закона от противного справедлива теорема  .
.
2. Теоремы вида 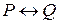 .
.
Мы уже знаем, что 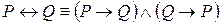 . Таким образом, это тот случай, когда истинна и теорема
. Таким образом, это тот случай, когда истинна и теорема  , и обратная ей теорема
, и обратная ей теорема  . Формулируется эта теорема с помощью парных союзов: «Для
. Формулируется эта теорема с помощью парных союзов: «Для 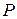 необходимо и достаточно
необходимо и достаточно 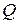 », «
», « 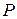 тогда и только тогда, когда
тогда и только тогда, когда 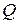 », «
», « 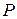 если и только если
если и только если 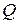 ». Укажем два способа доказательства таких теорем.
». Укажем два способа доказательства таких теорем.
1) Методом доказательство прямой и обратной теорем. При использовании этого метода для доказательства теоремы 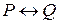 доказывают прямую теорему
доказывают прямую теорему  и называют это доказательством необходимости (
и называют это доказательством необходимости ( 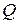 для
для 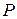 ), и обратную теорему
), и обратную теорему  и называют это доказательством достаточности (
и называют это доказательством достаточности ( 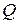 для
для 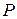 ).
).
Пример 3. Для того, чтобы целое число 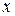 делилось на 15, необходимо и достаточно, чтобы
делилось на 15, необходимо и достаточно, чтобы 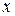 делилось на 3 и 5.
делилось на 3 и 5.
□ Соответствующая теорема имеет вид  , где
, где  есть предикат
есть предикат 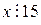 , а
, а 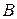 – предикат
– предикат 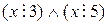 . Установим тождественную истинность в
. Установим тождественную истинность в 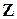 предиката
предиката
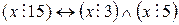 .
.
Необходимость. 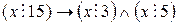 .
.
Докажем эту теорему с помощью цепочки истинных импликаций:
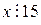
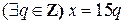
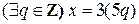
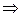
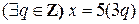
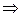
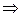
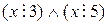 .
.
Достаточность.  .
.
Эта теорема будет вытекать из следующего свойства делимости взаимно простых чисел: если целое число 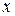 делится на каждое из взаимно простых целых чисел
делится на каждое из взаимно простых целых чисел 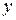 и
и 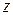 , то
, то 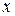 делится и на их произведение
делится и на их произведение 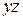 (оно будет доказано в курсах «Элементарная математика» и «Теория чисел»).
(оно будет доказано в курсах «Элементарная математика» и «Теория чисел»).
2) Доказательство с помощью цепочки истинных эквиваленций проводится по аналогии с доказательством при помощи цепочки истинных импликаций, основываясь на свойстве транзитивности эквиваленции.
Пример 4. Доказать, что 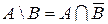 .
.
□ Основываясь на универсальном методе доказательства равенства двух множеств и на выражении логической равносильности через эквивалентность, достаточно показать, что 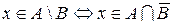 .
.
Имеем следующую цепочку логических эквивалентностей:
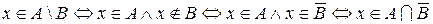 .
.
В самих теоремах вида  или
или  , как мы уже видели в примерах, предикаты
, как мы уже видели в примерах, предикаты  и
и 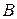 могут оказаться сложными, например,
могут оказаться сложными, например,  ,
, 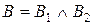 и т.д.
и т.д.
Дата добавления: 2015-11-04; просмотров: 5379;
