Логическое следование и логическая равносильность
Предикатов
Материал этого раздела во многом аналогичен материалу § 3 гл. I.
Определение 1. Говорят, что из предиката 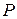 логически следует предикат
логически следует предикат 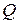 и пишут
и пишут 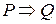 , если для всякого допустимого набора значений входящих в них переменных, всякий раз, когда значение предиката
, если для всякого допустимого набора значений входящих в них переменных, всякий раз, когда значение предиката 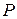 есть истинное высказывание, таковым является и значение предиката
есть истинное высказывание, таковым является и значение предиката 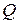 .
.
В случае, когда 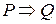 говорят также, что предикат
говорят также, что предикат 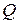 является логическим следствием предиката
является логическим следствием предиката 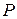 , или предикат
, или предикат 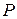 логически влечет предикат
логически влечет предикат 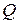 .
.
Обратим внимание на то, что знак следования 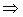 является не операцией над предикатами, а отношением между предикатами.
является не операцией над предикатами, а отношением между предикатами.
Легко понять, что справедлива
Т е о р е м а 1(о свойствах логического следования для предикатов).Дляпредикатов 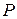 ,
, 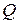 и
и 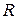 справедливы следующие свойства:
справедливы следующие свойства:
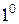 .
. 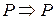 , т.е. отношение логического следования рефлексивно;
, т.е. отношение логического следования рефлексивно;
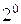 . если
. если 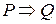 и
и 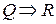 , то
, то 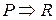 , т.е. отношение логического следования для предикатов транзитивно;
, т.е. отношение логического следования для предикатов транзитивно;
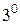 . из любого предиката
. из любого предиката 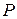 логически следует любой тождественно истинный предикат
логически следует любой тождественно истинный предикат 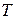 , т.е.
, т.е. 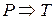 .
.
Полезно иметь в виду следующее утверждение:
Т е о р е м а 2 (признак логического следования для предикатов). Предикат 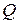 является логическим следствием предиката
является логическим следствием предиката 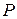 тогда и только тогда, когда импликация
тогда и только тогда, когда импликация 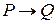 является тождественно истинным предикатом.
является тождественно истинным предикатом.
□ Пусть 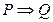 . Если для допустимого набора значений переменных логическое значение предиката
. Если для допустимого набора значений переменных логическое значение предиката 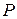 есть1, т.е.
есть1, т.е. 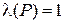 , то и
, то и 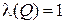 , а поэтому
, а поэтому 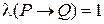 . Если
. Если 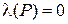 , то
, то 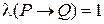 . Таким образом, в этом случае импликация
. Таким образом, в этом случае импликация 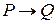 является тождественно истинным предикатом.
является тождественно истинным предикатом.
Пусть 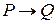 есть тождественно истинный предикат и предположим, что предикат
есть тождественно истинный предикат и предположим, что предикат 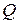 не является логическим следствием предиката
не является логическим следствием предиката 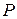 . Тогда существует такой допустимый набор значений переменных, что
. Тогда существует такой допустимый набор значений переменных, что 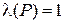 и
и 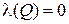 . Но тогда
. Но тогда 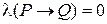 , что противоречит предположению.
, что противоречит предположению.
Определение 2. Говорят, что из предикатов 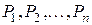 логически следует предикат
логически следует предикат 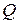 и пишут
и пишут 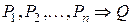 , если для любого набора значений
, если для любого набора значений 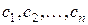 переменных
переменных 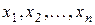 , входящих в запись формул
, входящих в запись формул 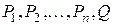 , высказывание
, высказывание 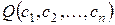 истинно всякий раз, когда все высказывания
истинно всякий раз, когда все высказывания 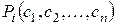
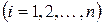 истинны.
истинны.
Например, очевидно, что 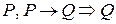 .
.
На самом деле, как показывает нижеследующая теорема, логическое следование из нескольких предикатов можно заменить логическим следованием из одного предиката.
Т е о р е м а 3 . Для того чтобы предикат 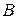 была логическим следствием предикатов
была логическим следствием предикатов 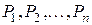 , необходимо и достаточно, чтобы предикат
, необходимо и достаточно, чтобы предикат 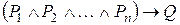 был тождественно истинным.
был тождественно истинным.
□Доказательствовытекаетиз определения конъюнкции и теоремы 2.
Определение 3. Два предиката 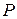 и
и 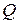 называются логически равносильными (пишут
называются логически равносильными (пишут 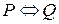 ), когда каждый из них является логическим следствием другого.
), когда каждый из них является логическим следствием другого.
Из определения 3 и теоремы 2 легко вытекает
Т е о р е м а 4 (признак логической равносильности для предикатов). Предикат 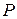 логически равносилен предикату
логически равносилен предикату 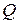 тогда и только тогда, когда эквиваленция
тогда и только тогда, когда эквиваленция 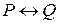 является тождественно истинным предикатом.
является тождественно истинным предикатом.
Замечание.Непосредственно из вышесказанного заключаем, что понятия равносильности предикатов совпадают с понятием логической равносильности, т.е. 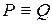 тогда и только тогда, когда
тогда и только тогда, когда 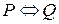 .
.
Дата добавления: 2015-11-04; просмотров: 3289;
