Операции над предикатами и основные равносильности
Для предикатов
Операции над высказываниями являются также и операциями над предикатами. Если 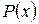 и
и 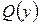 – одноместные предикаты, то
– одноместные предикаты, то 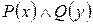 – тоже предикат (но уже 2-местный), который превращается в истинное высказывание при всех тех и только тех значениях переменных х, у, при которых значения предикатов
– тоже предикат (но уже 2-местный), который превращается в истинное высказывание при всех тех и только тех значениях переменных х, у, при которых значения предикатов 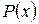 и
и 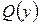 являются истинными высказываниями. Над предикатами естественным образом вводятся также операции отрицания, дизъюнкции, импликации и эквиваленции. В логике предикатов выполняются все равносильности алгебры высказываний. Но здесь есть и собственные равносильности, связанные с новыми операциями над предикатами – навешиванием кванторов общности и существования.
являются истинными высказываниями. Над предикатами естественным образом вводятся также операции отрицания, дизъюнкции, импликации и эквиваленции. В логике предикатов выполняются все равносильности алгебры высказываний. Но здесь есть и собственные равносильности, связанные с новыми операциями над предикатами – навешиванием кванторов общности и существования.
Пусть 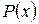 – одноместный предикат, D – ОДЗ переменной х и
– одноместный предикат, D – ОДЗ переменной х и 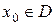 . Естественно говорить, что «элемент
. Естественно говорить, что «элемент 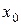 обладает свойством
обладает свойством 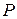 », когда высказывание
», когда высказывание 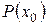 истинно, и «элемент
истинно, и «элемент 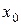 не обладает свойством
не обладает свойством 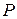 », когда высказывание
», когда высказывание 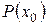 ложно.
ложно.
Обозначим через 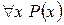 высказывание «для всех
высказывание «для всех  имеет место
имеет место 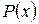 » Указанное высказывание истинно, если все элементы из D обладают свойством
» Указанное высказывание истинно, если все элементы из D обладают свойством 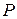 , и ложно, если, по крайней мере, один элемент из D не обладает этим свойством. Символ
, и ложно, если, по крайней мере, один элемент из D не обладает этим свойством. Символ 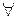 называют квантором общности, выражение
называют квантором общности, выражение 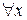 (или
(или 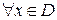 ) – квантором общности по переменной х, а саму операцию, в результате которой предикат
) – квантором общности по переменной х, а саму операцию, в результате которой предикат 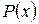 превращается в высказывание
превращается в высказывание 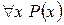 – навешиванием на предикат
– навешиванием на предикат 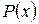 квантора общности по переменной х. Сведем сказанное в определение.
квантора общности по переменной х. Сведем сказанное в определение.
Определение 1.Переход от предиката 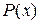 к высказыванию
к высказыванию 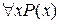 , которое читается «для всех
, которое читается «для всех  имеет место
имеет место 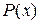 » и считается истинным, если предикат P(x) превращается в истинное высказывание для любого значения x из области определения P(x), называется операцией навешивания квантора общности
» и считается истинным, если предикат P(x) превращается в истинное высказывание для любого значения x из области определения P(x), называется операцией навешивания квантора общности 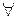 на предикат
на предикат 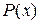 по переменной x.
по переменной x.
Аналогично, через 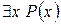 обозначим высказывание: «Существует такое
обозначим высказывание: «Существует такое  , что
, что 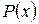 » Это высказывание означает, что в множестве
» Это высказывание означает, что в множестве 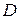 есть элемент, обладающий свойством Р. Оно ложно лишь в том случае, когда ни один элемент множества
есть элемент, обладающий свойством Р. Оно ложно лишь в том случае, когда ни один элемент множества 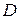 не обладает свойством Р. Символ
не обладает свойством Р. Символ 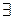 называется квантором существования, выражение
называется квантором существования, выражение 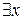 – квантором существования по переменной х, а операция, осуществляющая переход от предиката
– квантором существования по переменной х, а операция, осуществляющая переход от предиката 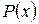 к высказыванию
к высказыванию 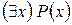 – навешиванием на предикат
– навешиванием на предикат 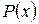 квантора существования по переменной
квантора существования по переменной  .
.
Подытожим сказанное в виде определения.
Определение 2.Переход от предиката 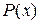 к высказыванию
к высказыванию  , которое читается «существует такое x, что имеет место
, которое читается «существует такое x, что имеет место 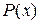 » и считается истинным, если предикат P(x) превращается в истинное высказывание хотя бы для одного значения x из области определения
» и считается истинным, если предикат P(x) превращается в истинное высказывание хотя бы для одного значения x из области определения 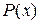 , называется операцией навешивания квантора существования
, называется операцией навешивания квантора существования 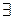 на предикат
на предикат 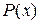 по переменной
по переменной  .
.
Договоримся еще, что 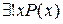 обозначает высказывание, которое читается «существует единственное x такое, что имеет место
обозначает высказывание, которое читается «существует единственное x такое, что имеет место 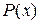 » и считается истинным, если предикат
» и считается истинным, если предикат 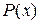 превращается в истинное высказывание только для одного значения
превращается в истинное высказывание только для одного значения  из области определения
из области определения 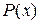 .
.
Если M является подмножеством множества D, то условимся через 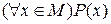 обозначать высказывание: «Для всех х из M имеет место
обозначать высказывание: «Для всех х из M имеет место 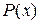 » и считать истинным, если предикат
» и считать истинным, если предикат 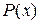 превращается в истинное высказывание для любого значения
превращается в истинное высказывание для любого значения  из множества M (операция навешивания ограниченного квантора общности на предикат
из множества M (операция навешивания ограниченного квантора общности на предикат 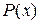 по переменной
по переменной  ). Аналогично через
). Аналогично через 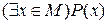 будем обозначать высказывание, которое читается «существует х из M такое, что
будем обозначать высказывание, которое читается «существует х из M такое, что 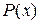 » и считается истинным, если предикат P(x) превращается в истинное высказывание хотя бы для одного значения x из множества M (операция навешивания ограниченного квантора существования на предикат
» и считается истинным, если предикат P(x) превращается в истинное высказывание хотя бы для одного значения x из множества M (операция навешивания ограниченного квантора существования на предикат 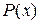 по переменной
по переменной  ).
).
Замечание 1.Понятно,чтовысказывание 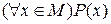 равносильно высказыванию
равносильно высказыванию 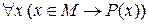 , а высказывание
, а высказывание 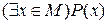 равносильно высказыванию
равносильно высказыванию 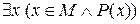 .
.
Пример 1. Пусть задан предикат 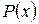 – «х является натуральным числом», причем множество Z является ОДЗ переменной
– «х является натуральным числом», причем множество Z является ОДЗ переменной  . Тогда
. Тогда 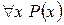 – ложное высказывание,
– ложное высказывание, 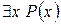 – истинное высказывание. С другой стороны, оба высказывания
– истинное высказывание. С другой стороны, оба высказывания 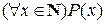 и
и 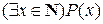 истинны.
истинны.
Если ОДЗ переменной  является конечное множество
является конечное множество 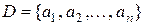 , то для любого предиката
, то для любого предиката 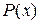 имеем:
имеем:
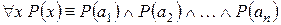 ,
,
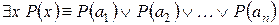 .
.
Отсюда видно, что квантор общности является обобщением конъюнкции, а квантор существования – обобщением дизъюнкции на бесконечные множества.
Понятно, что кванторы общности и существования можно навешивать на многоместные предикаты. При этом каждая операция навешивания квантора «связывает» одну переменную и уменьшает на единицу число свободных переменных предиката, т.е. получаем предикат от тех переменных, на которые кванторы не навешены. Если кванторы навешиваются на все переменные, то получается высказывание.
Пример 2. Рассмотрим двухместный предикат 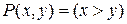 , где ОДЗ переменных
, где ОДЗ переменных  и
и 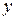 является множество R. Тогда
является множество R. Тогда 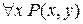 ,
, 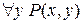 ,
, 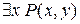 ,
, 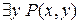 – одноместные предикаты, а
– одноместные предикаты, а 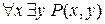 ,
, 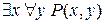 – высказывания, причем первое из них истинно, а второе – ложно.
– высказывания, причем первое из них истинно, а второе – ложно.
Замечание 2. Понятно, что одноименные кванторы можно менять местами. Как показывает пример 2, разноименные кванторы в общем случае менять местами нельзя.
В заключение этого раздела отметим некоторые равносильности предикатов, связанные с операциями навешивания кванторов. Для их формулировки условимся считать, что переменная  входит в предикаты P, Q свободно и писать
входит в предикаты P, Q свободно и писать 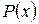 ,
, 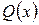 . Считаем также, что кванторы имеют приоритет перед всеми другими логическими операциями, т.е. применяются в первую очередь.
. Считаем также, что кванторы имеют приоритет перед всеми другими логическими операциями, т.е. применяются в первую очередь.
1. Законы отрицания кванторов (законы де Моргана):
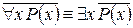 ,
, 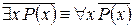 .
.
2. Законы выражения кванторов друг через друга:
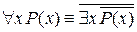 ;
; 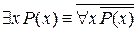 .
.
3.Законы пронесения кванторов через конъюнкцию и дизъюнкцию:
а) 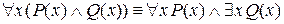
б) 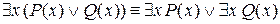 ;
;
в) 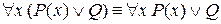 (Q – высказывание);
(Q – высказывание);
г) 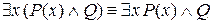 (Q – высказывание).
(Q – высказывание).
4. Законы пронесения кванторов через импликацию:
а) 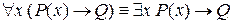 (Q – высказывание);
(Q – высказывание);
б) 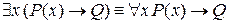 (Q – высказывание);
(Q – высказывание);
в) 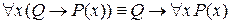 (Q – высказывание);
(Q – высказывание);
г) 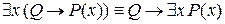 (Q – высказывание).
(Q – высказывание).
5. Законы удаления квантора общности и введения квантора существования:
а) 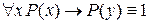 ;
;
б) 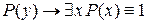 .
.
6. Законы коммутативности для кванторов:
а) 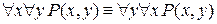 ;
;
б) 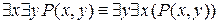 ;
;
в) 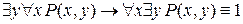 .
.
Интуитивно эти равносильности понятны, доказательство же их выходит за рамки нашего пособия.
Замечание 3. Если в равносильностях 1-6 считать, что предикаты зависят от произвольного конечного числа предметных переменных, то соответствующие предикаты будут также равносильны. В частности, понятно как распространить закон отрицания кванторов на многоместные предикаты, у которых кванторная приставка состоит из нескольких кванторов. А именно справедливо следующее правило: чтобы найти отрицание выражения, начинающегося с кванторов, надо каждый квантор общности заменить квантором существования и наоборот, а знак отрицания перенести за кванторы. С использованием этого правила, мы встретимся в дальнейшем.
Замечание 4.Ясно, что всякий предикат, получающийся из тавтологии алгебры высказываний заменой входящих в нее высказывательных переменных произвольными предикатами, будет тождественно истинным предикатом.
Дата добавления: 2015-11-04; просмотров: 3801;
