Выражение, переменная, форма, терм, предикат

Понятие выражения и переменной широко применяются в школьном курсе математики. Это первоначальные понятия, они не определяются, а описываются, разъясняются на примерах и уточняются. Продолжим процесс уточнения этих понятий.

Набор всех букв и знаков, употребляемых в математике, называется математическим алфавитом. Математический алфавит содержит буквы русского, латинского, греческого алфавитов, все цифры, знаки 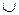, , 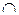, , 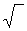, 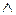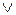<, >, +, –, = и т.д.

Выражение – это любая совокупность букв математического алфавита, записанная в некотором порядке и имеющая определенный смысл.

Переменная – это буква в выражении, вместо которой можно подставлять элементы некоторого множества, называемого областью изменения переменной. Иногда та или иная буква в выражении объявляется переменной специальным указанием, в других случаях это может быть видно из самого выражения или из предшествующего текста. Обычно переменные обозначаются буквами латинского алфавита x, y, z и т.д. Объявляя ту или иную букву переменной, надо указать и область ее изменения. Те значения переменной из области ее изменения, после подстановки которых выражение имеет смысл, называются допустимыми значениями, а множество допустимых значений – областью допустимых значений переменной (ОДЗ). Например, если 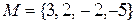– область изменения переменной x в выражении 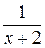, то ОДЗ есть множество .

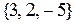Выражения, содержащие переменные, называются формами, а не содержащие переменные – константами. Форма, содержащая s переменных, называется s-местной.

Важнейшими классами констант являются классы числовых выражений и высказываний. Примерами числовых выражений являются, например, выражения 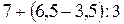, , 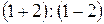и т.д. Если выполнить все операции в числовом выражении, то получится число, которое называется значением этого выражения. Примеры высказываний нам также известны.

Важнейшими классами форм являются классы числовых форм и класс высказывательных форм. Форма называется высказывательной, или предикатом, если при любом наборе допустимых значений переменных она обозначает высказывание. В дальнейшем мы отдаем предпочтение термину предикат, имея в виду сложившуюся терминологию в математической логике, систематический курс которой будет изучаться в дальнейшем. Подчеркнем, что сами допустимые значения переменных предиката не обязательно должны быть высказываниями. Так, уравнение 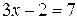есть предикат, который при 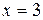является истинным высказыванием, а при всех остальных действительных значениях x – ложным. Переменная х в этом предикате принимает числовые значения. Очевидно, что все уравнения и неравенства, а также системы уравнений и неравенств, являются предикатами. В школьном курсе математики предикаты называют предложениями с переменной. Будем говорить, что два предиката принимают одинаковые значения для данного набора значений входящих в них переменных, если совпадают истинностные значения соответствующих высказываний.

Определение 1. Два выражения называются равносильными, если при любом наборе значений входящих в них переменных, либо оба они не определены, либо оба определены и имеют одинаковое значение.

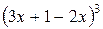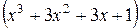Например, равносильными являются числовые формы и . Числовая форма 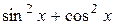равносильна константе 1, числовое выражение 4:2 равносильно 8:4. Любые два истинных высказывания, также как и любые два ложных высказывания, равносильны между собой.

Для обозначения равносильности предикатов и высказываний будем пользоваться знаком ≡. Например,

, .

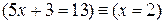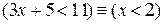Очевидно, что равносильность уравнений и неравенств, а также систем уравнений и неравенств – это частный случай равносильности предикатов.

Выражения, не содержащие знаков отношений (=, ≤, ≥, <, > и т.д.), будем называть термами, а все выражения, содержащие по крайней мере один из этих знаков – формулами логики предикатов или предикатными формулами. Например, выражение 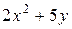– терм, а выражение 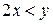–формула. Таким образом, если два терма соединить каким-либо знаком отношения, то получится формула (такие формулы называются элементарными). Применяя к элементарным формулам известные логические операции отрицания конъюнкции, дизъюнкции, импликации и эквиваленции, а также операции навешивания кванторов общности и существования, которые будут рассмотрены в следующем параграфе, снова получаем сложные предикатные формулы. Например, 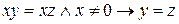– формула, выражающая свойство сократимости операции умножения чисел. Понятно, что любая формула является предикатом.

Заметим, что одноместная числовая форма каждому значению переменной ставит в соответствие вполне определенное число, т.е. определяет некоторую числовую функцию. Аналогично, одноместный предикат каждому значению переменной ставит в соответствие ложное высказывание или истинное высказывание. Если заменить высказывания их истинностными значениями, то можно сказать, что одноместный предикат определяет функцию, которая принимает значения из множества 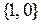. Эту функцию называют логической функцией. Многоместные высказывательные формы определяют логические функции от нескольких переменных. Понятно, что два предиката равносильны тогда и только тогда, когда они определяют одну и туже логическую функцию.

Определение 2.Предикат 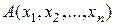называется тождественно истинным, если для любого допустимого набора 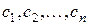значений переменных 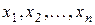его значение 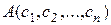является истинным высказыванием.

Например, предикат 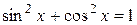является тождественно истинным в R.

Определение 3.Предикат 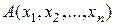называется тождественно ложным, если для любого допустимого набора 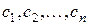значений переменных 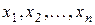его значение 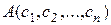является ложным высказыванием.

Например, предикат 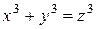, как известно, является тождественно ложным в N.

Определение 4.Предикат 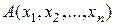называется выполнимым, если для некоторого допустимого набора 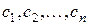значений переменных 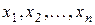его значение 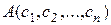является истинным высказыванием.

Определение 5.Предикат 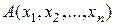называется опровержимым, если для некоторого допустимого набора 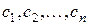значений переменных 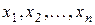его значение 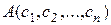является ложным высказыванием.

Например, формула 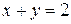является одновременно выполнимой и опровержимой в R .