Правильные и неправильные рассуждения
Одной из главных задач логики является анализ рассуждений. Под рассуждением будем понимать вывод из некоторых высказываний, называемых посылками, нового высказывания – заключения.
Рассуждение считается правильным лишь тогда, когда с его помощью из истинных посылок нельзя получить ложное заключение. Законы логики, выражаемые тавтологиями алгебры высказываний, служат основой для выводов, в которых учитывается только вид (структура) сложных высказываний или предикатов с точностью до элементарных высказываний или предикатов. Элементарные высказывания логика высказываний не анализирует, также как и логика предикатов не анализирует элементарные предикаты.
Правила вывода – это предписания, позволяющие признавать правильными высказывания в зависимости от того, какой вид имеют высказывания, уже признанные истинными (посылки).
Посылки от следствия обычно разделяют словом «следовательно».
Правило отделения (заключения или modus ponens)было известно уже в древности в школе стоиков. Оно заключается в следующем. Мы делаем правильное умозаключение, если из двух посылок вида
1. если P, то Q ( 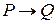 ).
).
2. P
получаем в качестве вывода (заключения), что
3. Q.
Это же короче можно сказать так: наше рассуждение правильно, если из двух посылок, среди которых одна является импликацией, а другая совпадает с условием этой импликации, мы выводим предложение, совпадающее с заключением той же импликации. Сказанное можно записать так 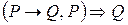 и обосновать, установив тождественную истинность предиката
и обосновать, установив тождественную истинность предиката 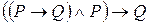 .
.
Мы утверждаем правильность умозаключения, принимая во внимание только вид посылок (их форму), содержание же посылок может быть самым разнообразным.
Правило отделения повсеместно употребляется в математических доказательствах и житейской практике.
Рассмотрим применение правила отделения на примерах из математической и житейской практики.
Пример 1.
1. Если число  оканчивается нулем, то
оканчивается нулем, то  делится на 5 (
делится на 5 ( 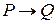 ).
).
2. Число  оканчивается нулем (P).
оканчивается нулем (P).
3. Следовательно,  делится на 5 (Q).
делится на 5 (Q).
Пример 2.
1. Если завтра будет дождь, то завтра концерт в парке не состоится ( 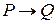 ).
).
2. Завтра будет дождь (P).
3. Следовательно, завтра концерт в парке не состоится (Q).
В этих примерах содержание разное, а форма рассуждения одна и та же. Если признать истинными посылки 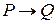 , P, то истинным будет и Q.
, P, то истинным будет и Q.
Обычно посылки пишут над чертой, а заключение под чертой. Правило отделения можно записать так:
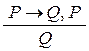 (правило отделения).
(правило отделения).
Укажем еще некоторые правила вывода, применяющиеся в логико-математической практике.
Правило силлогизма: 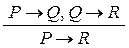 .
.
Это правило обосновано ранее.
Правило отрицания: 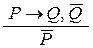 .
.
□ Для обоснования этого правила покажем, что 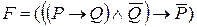 – тождественно истинный предикат. Пусть для некоторого набора значений переменных, входящих в запись предикатов P и Q , имеет место
– тождественно истинный предикат. Пусть для некоторого набора значений переменных, входящих в запись предикатов P и Q , имеет место 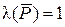 (напомним, что для высказывания
(напомним, что для высказывания 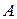 через
через 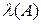 обозначается его логическое значение). Тогда по определению импликации
обозначается его логическое значение). Тогда по определению импликации 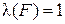 . Пусть
. Пусть 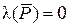 . Тогда
. Тогда 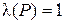 . Если
. Если 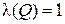 , то
, то 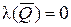 и поэтому
и поэтому 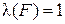 . Если
. Если 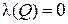 , то
, то 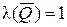 ,
, 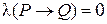 и поэтому
и поэтому 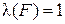 . Итак, рассуждение по правилу отрицания является правильным.
. Итак, рассуждение по правилу отрицания является правильным.
Рассмотрим применение правила отрицания на примере из математической практики.
Пример 3.
1. Если десятичная запись числа  оканчивается цифрой 6, то
оканчивается цифрой 6, то 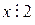 .
.
2. Число  не делится на 2.
не делится на 2.
3. Следовательно,  не оканчивается цифрой 6.
не оканчивается цифрой 6.
Приведем теперь пример неправильного рассуждения.
Пример 4. Рассмотрим следующее рассуждение:
1. Если четырехугольник – параллелограмм, то его противоположные стороны попарно параллельны
2. Если четырехугольник – квадрат, то его противоположные стороны попарно параллельны
3. Следовательно, если четырехугольник – квадрат, то он параллелограмм.
Обозначим высказывание «четырехугольник – параллелограмм» буквой P, «четырехугольник – квадрат» буквой Q, «противоположные стороны попарно параллельны» – буквой R. Наше рассуждение построено по схеме
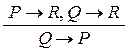 .
.
В нашем конкретном примере мы пришли к правильному выводу. Покажем, что рассуждение по указанной схеме не является правильным. Пусть для некоторого набора значений переменных, входящих в запись предикатов P, Q и R имеет место 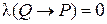 . Тогда по определению импликации
. Тогда по определению импликации 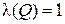 и
и 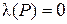 . Если
. Если 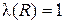 , то
, то 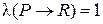 ,
, 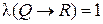 и
и 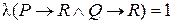 . Таким образом, если
. Таким образом, если 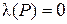 ,
, 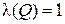 ,
, 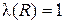 , то посылки
, то посылки 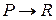 и
и 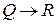 – истинны, а заключение
– истинны, а заключение 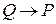 – ложно. Поэтому наше рассуждение ошибочно. Поэтому указанная схема не является правилом вывода.
– ложно. Поэтому наше рассуждение ошибочно. Поэтому указанная схема не является правилом вывода.
Проиллюстрируем это на следующем рассуждении:
1. Если четырехугольник – параллелограмм (P), то он имеет две параллельные стороны (R).
2. Если четырехугольник – трапеция (Q), то он имеет две параллельные стороны (R).
3. Следовательно, если четырехугольник – трапеция (Q), то он параллелограмм (P).
В данном случае, рассуждая по той же схеме, мы пришли к неправильному выводу.
Упражнение 1. Обосновать следующее правило вывода (записать в виде тождественно-истинной формулы закон логики, лежащий в основе этого правила вывода):
правило расширенной контрапозиции: 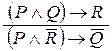 .
.
Упражнение 2.Провести анализ рассуждения. Если натуральное число  делится на 2 и на 3, то
делится на 2 и на 3, то  делится на 6. Следовательно, если натуральное число
делится на 6. Следовательно, если натуральное число  делится на 2 и не делится на 6, то оно не делится на 3.
делится на 2 и не делится на 6, то оно не делится на 3.
Упражнение 3.В системеN0неотрицательных целых чиселдать обоснованные ответы на вопрос: следует ли из посылок заключение?
| Посылки | Заключения | |
| а) | 1. Если число оканчивается нулем, то оно делится на 5. 2. Число не оканчивается нулем. | Число не делится на 5. |
| б) | 1. Если число оканчивается нулем, то оно делится на 5. 2. Число делится на 5. | Число оканчивается нулем. |
| в) | 1. Если 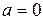 или или 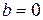 , то , то 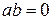 .
2. .
2. 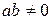
| 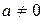 и и 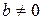
|
Упражнение 4.На предприятии есть три отдела 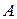 ,
, 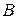 ,
, 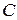 , договорившиеся о следующем утверждении проектов: а) если отдел
, договорившиеся о следующем утверждении проектов: а) если отдел 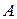 не участвует в утверждении проекта, то в этом утверждении не участвует и отдел
не участвует в утверждении проекта, то в этом утверждении не участвует и отдел 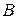 ; б)если отдел
; б)если отдел 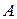 участвует в утверждении проекта, то в нем участвуют отделы
участвует в утверждении проекта, то в нем участвуют отделы 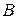 и
и 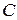 . Выяснить, обязан ли при этих условиях отдел
. Выяснить, обязан ли при этих условиях отдел 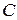 участвовать в утверждении проекта, когда в нем участвует отдел
участвовать в утверждении проекта, когда в нем участвует отдел 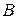 .
.
Дата добавления: 2015-11-04; просмотров: 5874;
