Умозаключения (рассуждения) и их виды
Большую часть знаний об окружающей нас действительности мы получаем с помощью рассуждений. Выводы в них будут истинными, если они являются результатами правильных рассуждений. Правильными рассуждениями считают рассуждения, построенные по правилам логики. Учителю нужны знания о тех правилах, в соответствии с которыми строятся правильные рассуждения. Рассуждения лежат в основе доказательств, без которых трудно представить математику.
В логике наряду с термином «рассуждение» используется термин «умозаключение».
Умозаключением (рассуждением) называется логическая операция, в результате которой получают новое знание на основе некоторого имеющегося знания или из некоторых утверждений А1, А 2, А 3, А 4 … А n (n > 1) получают новое по отношению к исходным, утверждение В.
Умозаключение состоит из посылок и заключения.
Посылки умозаключения – это исходные утверждения, а заключением называется новое утверждение, т.е. утверждение, содержащее новое знание.
В логике принято указывать вначале посылки, а потом заключение, но в конкретном умозаключении их порядок может быть произвольным: вначале заключение – потом посылки; заключение может находиться между посылками.
Пример 1. Из двух утверждений «Все жидкости упруги» и «Вода – жидкость», можно получить новое утверждение следующим образом: «Все жидкости упруги. Вода – жидкость, значит, вода упруга». Здесь исходные утверждения «Все жидкости упруги» и «Вода – жидкость» являются посылками, а новое утверждение «Вода упруга» является заключением умозаключения.
Рассмотрим примеры умозаключений, которые выполняют младшие школьники при изучении математики.
Пример 2. Ученику предлагается объяснить, почему число 35 можно представить в виде суммы 30 и 5. Он рассуждает: «Число 23 – двухзначное. Любое двухзначное число можно представить в виде суммы разрядных слагаемых. Следовательно, 35=30+5».
В этом умозаключении первое и второе предложения – посылки, причем первая – частная (характеризует только 35), а вторая – общего характера; заключение – это часть предложения, которая стоит после слова «следовательно», причем заключение носит частный характер.
Пример 3. Один из приемов ознакомления с переместительным свойством умножения заключается в следующем. Используя различные средства наглядности, школьники вместе с учителем устанавливают, что, например, 2∙5=5∙2, 6∙3=3∙6, 4∙7=7∙4. А затем на основе полученных равенств делают вывод: для всех натуральных чисел а и в верно равенство а∙в=в∙а.
В данном умозаключении посылками являются первые три равенства, в которых утверждается, что для конкретных натуральных чисел выполняется такое свойство, т.е. посылки будут частными. Заключением является утверждение общего характера – сделанный вывод.
Как видно из рассмотренных примеров, умозаключения бывают разные. В примерах 1 и 2 заключение логически следует из посылок, и мы не сомневаемся в его истинности.
В зависимости от того, существует ли между посылками и заключением отношение логического следования, выделяют два вида умозаключений: дедуктивные (лат. слово «deduction» означает «выведение»), которые в логике считают правильными и недедуктивные (неправильные).
Дедуктивным умозаключением называется умозаключение, в котором посылки и заключение находятся в отношении логического следования, т.е. во всех случаях, когда посылки истинны, заключение тоже истинно.
Если посылки умозаключения обозначить буквами А1,А2,... Аn, а заключение - буквой В, то схематично умозаключение можно представить в виде: А1,А2,...Аn⇒В.
Используют в логике и такую запись 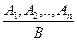 . Черта в данной записи заменяет слово «следовательно» («значит»).
. Черта в данной записи заменяет слово «следовательно» («значит»).
В дедуктивном умозаключении из истинных посылок всегда следует истинное заключение. К дедуктивным умозаключениям относятся, например, следующие:
Пример 4. «Если идет дождь, то земля становится мокрой. Идет дождь. Следовательно, земля мокрая».
Пример 5.  . Пример 6.
. Пример 6. 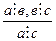 .
.
Пример 7. Если х∶2, то х - четное число. Число 2002∶2.
Число 2002 - четное.
Пример 8. Если х∶9, то х∶3. Число 122 не делится на 3.
Число 122 не делится на 9.
Правильность умозаключения определяется его формой, а не истинностью входящих в него утверждений. При анализе правильности умозаключения необходимо помнить о том, что нельзя отождествлять правильность умозаключения с истинностью полученного вывода. В логике существуют правила, соблюдая которые, можно строить дедуктивные умозаключения. Эти правила называют правилами вывода или схемами дедуктивных умозаключений.
Наиболее часто встречаются следующие схемы дедуктивных умозаключений:
1. А(х)⇒В(х), А(а) - правило заключения;
В(а)
2. А(х)⇒В(х), В(а) - правило отрицания;
А(а)
3. А(х)⇒В(х), В(х)⇒С(х) - правило силлогизма.
А(х)⇒С(х)
В рассмотренных примерах 4 и 7 умозаключение построено по правилу заключения, в примерах 5 и 6 – по правилу силлогизма, в примере 8 – по правилу отрицания, значит все они дедуктивные умозаключения.
Приведем примеры умозаключений (рассуждений).
1) Нетрудно убедиться в истинности следующих высказываний:
3 + 2 < 3 · 2 (А1),
4 + 3 < 4 · 3 (А 2),
7 + 5 < 7 · 5 ( А 3).
На их основе можно сделать вывод (В): сумма двух любых натуральных чисел всегда меньше их произведения.
2) Если число х при счете называют раньше числа у, то х меньше у (А1). Число 7 называют при счете раньше числа 8 (А 2). Следовательно, 7 < 8 (В).
Правильно строить дедуктивные умозаключения, анализировать их помогают правила логики:
| Правило заключения: (А (х) Þ В (х), А (а)) Þ В (а). |
Утверждение А (х) Þ В (х) называют общей посылкой, А (а) – частной посылкой, В (а) – заключением. По этому правилу выполнено умозаключение в примере 2.
| Общая посылка: А (х;у) Þ В (х;у) | Если число х называют при счете раньше числа у, то х < у. |
| Частная посылка: А (а;b) | Число 7 называют при счете раньше числа 8. |
| Заключение: В (а;b) | 7 < 8. |
Приведем пример использования этого правила в работе с дошкольниками.
Имеется одинаковое число чашек и блюдец.
Задание ребенку: «Покажи, что чашек столько же, сколько блюдец».
Рассуждения ребенка: «Поставим на каждое блюдце чашку».
| Общая посылка: А (х) Þ В (х) | Если можно образовать пары (чашка – блюдце), то предметов поровну. |
| Частная посылка: А (а) | На каждом блюдце стоит чашка, все блюдца заняты, и нет чашек без блюдца, т.е. из чашек и блюдец можно образовать пары. |
| Заключение: В (а) | Чашек и блюдец поровну. |
| Правило отрицания: (А (х) Þ В (х), В (а)) Þ А (а). |
Приведем пример умозаключения по этому правилу:
| Общая посылка: А (х) Þ В (х) | Если запись числа х оканчивается цифрой 5, то число х делится на 5. |
| Частная посылка: В (а) | Число 17 не делится на 5. |
| Заключение: А (а) | Запись числа 17 не оканчивается цифрой 5. |
Рассмотрим пример использования правила отрицания в работе с дошкольниками.
Имеется несколько чашек и блюдец.
Задание ребенку: «Установи, поровну ли чашек и блюдец».
Рассуждения ребенка: «На одном блюдце нет чашки, значит блюдец больше, чем чашек».
| Общая посылка: А (х) Þ В (х) | Если предметов поровну, то можно образовать пары (чашка – блюдце). |
| Частная посылка: В (а) | Для одного блюдца нет пары. |
| Заключение: А (а) | Блюдец и чашек не поровну. |
Ошибки в рассуждениях, неправильные чертежи, неумение использовать теоремы и формулы приводят к ложному заключению.
Математики стали специально придумывать умышленно неправильные рассуждения, имеющие видимость правильного. Такие рассуждения называются софизмы. Разбор софизмов формирует умение правильно рассуждать, помогает усваивать многие математические факты.
Пример:
Верно ли равенство? 25 + 35 – 60 = 30 + 42 – 72
Вынесем общий множитель за скобку. 5 · (5 + 7 – 12) = 6 · (5 + 7 – 12)
Разделим правую и левую часть 5 = 6
равенства на выражение в скобках.
Где ошибка? На 0 делить нельзя !
Существуют умозаключения, отличные от дедуктивных. Примером таких умозаключений могут быть неполная индукция и аналогия.
Неполная индукция– это умозаключение, при котором на основании того, что некоторые объекты совокупности обладают определенным свойством, делается вывод, что этим свойством обладают все объекты этой совокупности.
Примером неполной индукции является умозаключение в примере 1. Выводы в таких умозаключениях могут быть как истинными, так и ложными. В примере 1 заключение ложное.
Чтобы в этом убедиться, достаточно привести контрпример:
числа 3 и 1 – натуральные, 3 + 1 = 4, 3 · 1 = 3, 4 не меньше 3, т.е. нашлись два натуральных числа, сумма которых не меньше их произведения.
Рассмотрим еще один пример использования неполной индукции. Известно, что 15 делится на 5, 25 делится на 5, 35 делится на 5. Следовательно, можно утверждать, что любое число, запись которого оканчивается цифрой5, делится на 5. В данном случае заключение истинно – нам известен признак делимости на 5.
Выводы, получаемые при неполной индукции носит характер предположения, гипотезы. Их надо доказывать или опровергать.
Велика роль неполной индукции как способа получения общего знания, как способ открытия закономерностей, правил. Использование неполной индукции в обучении способствует развитию умений сравнивать, обобщать, делать выводы.
Приведем пример использования неполной индукции в работе с дошкольниками:
Наглядный материал: «Чудесный мешочек» с объемными геометрическими фигурами.
Задание ребенку: «Достань одну фигуру и назови».
Варианты ответов: - шар,
- шар,
- шар.
- Здесь, наверное, все шары.
Иногда при обучении дошкольников используют вывод по аналогии, при котором осуществляют перенос знаний с изученного объекта на другой, менее изученный объект.
Пример:
1) «У четырехугольника 4 угла и 4 стороны, следовательно у пятиугольника 5 углов и 5 сторон».
2) 
 «Если треугольник разделит пополам,
«Если треугольник разделит пополам,
получится два треугольника, следовательно,
если квадрат разделить пополам получится
два квадрата» (рис. 10). Рис. 9
Выводы полученные по аналогии могут быть истинными или ложными, их надо доказывать дедуктивным способом или опровергать контрпримером. Аналогия важна тем, что наводит нас на догадки, способствует развитию математической интуиции.
Задание 1.Назовите существенные свойства А В
Фигуры, изображенной на рисунке 2.
Д Рис.2 С
Дата добавления: 2015-10-19; просмотров: 3613;
