Отношения логического следования и равносильности между высказывательными формами

Понятие отношения логического следования высказывательных форм связано с операцией импликации этих форм.

Пусть на множестве Х заданы высказывательные формы А(х) и В(х).

Импликацией высказывательных форм А(х) и В(х), заданных на множестве Х, называется высказывательная форма А(х)⇒В(х), заданная на том же множестве, которая ложна при тех значениях х∊Х, при которых форма А(х) истинна, а В(х) ложна.

Обозначение А(х)⇒В(х), читаем: «Импликация А(х) и В(х)», или «Если А(х), то В(х)», т.е. импликация высказывательных форм образуется с помощью логической связки «если..., то...», причем А(х) называют условием, а В(х) – заключением.

Например, из высказывательных форм А(х): «х∶3» и В(х): «х∶4», х∊N, составим высказывательную форму А(х)⇒В(х): «Если х∶3, то х∶4», х∊N. Эта высказывательная форма истинна при некоторых значениях х и ложна при других. Подставим вместо х несколько натуральных значений:

1) при х = 12 имеем импликацию высказываний: «Если 12∶3, то 12∶4», которая истинна, т.к. условие «12∶3» и заключение «12∶4» - истинны;

2) при х = 16 получим : «Если 16∶3, то 16∶4», эта импликация также истинна, т.к. её условие «16∶3» - ложно, а заключение «16∶4»- истинно;

3) при х = 15 получим: «Если 15∶3, то 15∶4», эта импликация ложна, т.к её условие «15∶3» - истинно, а заключение «15∶4» - ложно;

4) при х = 17 имеем импликацию высказываний: «Если 17∶3, то 17∶4», которая ложна, т.к. условие «17∶3» и заключение «17∶4» - ложны.

В математике часто встречаются импликации высказывательных форм, которые истинны при любых значениях х из области определения Х.

Например, из высказывательных форм А(х): «х∶4» и В(х): «х∶2», х∊N, составим высказывательную форму А(х)⇒В(х): «Если х∶4, то х∶2», х∊N». Чтобы получить разные комбинации значений истинности для её условия и заключения, поставим вместо х натуральные значения:

1) при х = 5 получим: «Если 5∶4, то 5∶2», эта импликация истинна, т.к. её условие и заключение ложны;

2) при х = 6 получим: «Если 6∶4, то 6∶2», что тоже истинно, т. к условие – ложно, а заключение – истинно;

3) при х = 8 имеем: «Если 8∶4, то 8∶2», эта импликация опять истинна, т.к. условие и заключение истинны.

Нужно отметить, что в этот примере для х нельзя найти такое значение, чтобы условие стало истинным высказыванием, а заключение - ложным, т.к. нет числа, которое бы делилось на 4, но не делилось на 2. Таким образом, высказывательная форма «Если х∶4, то х∶2» истинна при любых значениях х∊N, причем не трудно заметить, что множество истинности Т_А условия «х∶4» является подмножеством множества истинности Т_В заключения «х∶2», т.е. Т_А 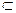Т_В. На основании выше изложенного можно сформулировать вывод.

Высказывательная форма А(х)⇒В(х), х∊Х, истинна тогда и только тогда, когда множество истинности Т_А высказывательной формы А(х) включается в множество истинности Т_В высказывательной формы В(х), т.е. когда при всех значениях х из множества Т_А 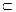Т_В .

Этим фактом удобно пользоваться при установлении значения истинности высказывательной формы А(х)⇒В(х).

Например, рассмотрим импликацию «Если число х – натуральное, то х – целое», х∊R. Для условия «Число х – натуральное» множество истинности Т_А = N, а для заключения - Т_В = Z. Как известно, множество N натуральных чисел включается во множество Z целых чисел, т.е. N 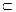Z, следовательно, данная импликация истинна при любых значениях х из множества R действительных чисел.

Если импликация А(х)⇒В(х), х∊Х, истинна при всех значениях х из множества Х, то говорят, что высказывательная форма В(х) логически следует из высказывательной формы А(х), и форму В(х) называют необходимым условием для высказывательной формы А(х), а форму А(х) – достаточным условием для высказывательной формы В(х).

Таким образом, мы определили отношение логического следования между высказывательными формами.

Высказывательную форму А(х)⇒В(х), которая является истинным высказыванием, можно прочитать по разному:

1) А(х) есть достаточное условие для В(х);

2) В(х) есть необходимое условие для А(х);

3) Всякое А(х) есть В (х);

4) В(х) логически следует из А(х);

5) Из А(х) логически следует В(х).

В рассмотренной ранее высказывательной форме А(х)⇒В(х): «Если х∶4, то х∶2», х∊N, высказывательная форма «х∶2» логически следует из формы «х∶4», причем «х∶2» является необходимым условием для «х∶4», а «х∶4» является достаточным условием для формы «х∶2». Используя эти терминалы, высказывательную форму «Если х∶4, то х∶2» можно переформулировать следующим образом:

1) для того чтобы х делилось на 4 необходимо, чтобы х делилось на 2;

2) для того чтобы х делилось на 2, достаточно, чтобы х делилось на 4;

3) всякое число, кратное 4, кратно и 2;

4) х∶2 логически следует из того, что х∶4;

5) из того, что х∶4 логически следует, что х∶2.

Для того чтобы показать, что высказывательные формы А(х) и В(х), заданные на множестве Х, не находятся в отношении логического следования, нужно указать такое значение а∊Х, при котором высказывание А(а) – истинно, а В(а) – ложно), т.е. привести контрпример.

Понятие отношения равносильности высказывательных форм связано с эквиваленцией этих форм.

Пусть на множестве Х заданы высказывательные формы А(х) и В(х).

Эквиваленцией высказывательных форм А(х) и В(х), заданных на множестве Х, называется высказывательная форма А(х)⇔В(х), заданная на том же множестве, которая истинна при тех значениях х, при которых обе формы А(х) и В(х) истинны или ложны одновременно.

Обозначение А(х)⇔В(х), х∊Х, читаем: «Эквиваленция А(х) и В(х)» или «А(х) тогда и только тогда, когда В(х)», т.е. эквиваленция высказывательных форм образуется с помощью логической связки, «... тогда и только тогда, когда ...». Может использоваться при чтении также логическая связка «...в том и только в том случае, если...».

Например, из высказывательных форм А(х): «Число х∶10» и В(х): «Десятичная запись числа х оканчивается нулем», х∊N, образуем высказывательную форму А(х)⇔В(х): «Число х делится на 10 тогда и только тогда, когда десятичная запись числа х оканчивается нулем». Подставим вместо х несколько натуральных значений:

1) при х = 30 имеем эквиваленцию высказываний «Число 30 делится на 10 тогда и только тогда, когда десятичная запись числа 30 оканчивается нулем», которая истинна, т.к. оба элементарные высказывания истинны;

2) при х = 45 имеем эквиваленцию: «Число 45 делится на 10 тогда и только тогда, когда десятичная запись числа 45 оканчивается нулем», которая тоже истинна, т.к. оба высказывания ложны.

Для рассматриваемой эквиваленции нет таких значений, при которых высказывательные формы принимали бы разные значения истинности («и» и «л» или «л» и «и»). Таким образом, эквиваленция «Число х делится на 10 тогда и только тогда, когда десятичная запись числа х заканчивается нулем» истинна при любых значениях х, причем множества истинности Т_А и Т_В составляющих высказывательных форм совпадают, т.е. Т_А = Т_В .

Высказывательная форма А(х)⇔В(х), х∊Х, истинна тогда и только тогда, когда множества истинности Т_А и Т_В составляющих высказывательных форм равны, т.е. Т_А = Т_В .

Этот факт можно использовать при установлении значения истинности высказывательной формы А(х)⇔В(х), х∊Х.

Например, рассмотрим эквиваленцию «х∶15⇔х∶3∧х∶5», х∊Х= {1;2;3;...;30}. Множество истинности Т_А формы «х∶5» будет равно: Т_А = {15; 30}, множество истинности Т_В высказывательной формы «х∶3 и х∶5» находится пересечением множеств истинности Т₁ и Т₂ составляющих форм «х∶3» и «х∶5»: Т_В = Т₁∩Т₂ = {3;6;9;12;15;18;21;24;27;30}∩{5;10;15;20;25;30} = {15;30}. Таким образом,получаем, что Т_А = Т_В, следовательно, данная эквиваленция истинна при любых значениях х из множества Х.

Если эквиваленция А(х) ⇔В(х), х∊Х, истинна при любых значениях х из множества Х, то высказывательные формы А(х) и В(х) находятся в отношении равносильности (или, короче, равносильны), и каждую форму называют необходимым и достаточным условием для другой.

В рассмотренной выше эквиваленции «х∶15⇔х∶3∧х∶5» составляющие её высказывательные формы «х∶15» и «х∶3 и х∶5» равносильны, поэтому иначе она может быть сформулирована следующим образом: «Для того чтобы х делилось на 15, необходимо и достаточно, чтобы х делилось на 3 и х делилось на 5».

Для того чтобы показать, что высказывательные формы А(х) и В(х), заданные на множестве Х, не находятся в отношении равносильности, нужно указать такое значение а 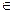Х, при котором высказывания А(а) и В(а) принимают разные значения истинности. («и» и «л» или «л» и «и»), т.е. привести контрпример.

Итак, мы рассмотрели отношения логического следования и равносильности между высказывательными формами, а также способы установления наличия этих отношений: 1) по выявлению отношения включения или равенства соответственно между множествами истинности этих форм; 2)по возможности приведения контрпримера.

Замечание. Отношения логического следования и равносильности были рассмотрены нами для одноместных высказывательных форм. Для высказывательных форм, содержащих две или более переменных, эти понятия определяются аналогично.