Отрицание высказывательной формы (предиката). Множество истинности отрицания

Высказывательные формы (предикаты), так же как и высказывания, бывают элементарными и составными. Составные высказывательные формы образуются из элементарных при помощи тех же логических связок, которые используются в составных высказываниях.

Пусть на множестве Х задана высказывательная форма А(х).

Отрицанием высказывательной формы (предиката) А(х), заданной на множестве Х, называется высказывательная форма Ā(х), заданная на том же множестве, которая истинна при тех значениях хÎХ, при которых данная форма А(х) ложна, и, наоборот, ложна при тех значениях хÎХ, при которых данная форма А(х) истинна.

Обозначение Ā(х) читаем: «Неверно, что А от х» или «Не А от х».

Например, пусть дана высказывательная форма А(х): «хM3», где хÎХ={1; 2; 3; 4; 5; 6; 7}. Найдем ее множество истинности: Т_А ={3;6}. Сформулируем отрицание данной формы Ā(х): «Неверно, что хM3» или, иначе, Ā(х): «х не делится на 3». Множеством истинности Ā(х) является множество Т_Ā={1;2;4;5;7}. Не трудно заметить, что это множество является дополнением к множеству Т_А до множества Х, т.е. эти множества изображаются на диаграмме Эйлера-Венна следующим образом (рис. 19).

Х Т_Ā

T_A

Рис. 19

Таким образом, сформулируем правило нахождения множества истинности отрицания высказывательной формы Ā(х), если известно множество истинности данной формы А(х).

Если Т_А - множество истинности высказывательной формы А(х), хÎХ, то множеством истинности Т_Ā - высказывательной формы Ā(x), хÎX, является дополнение к множеству Т_А до области определения Х, т.е.

Т_Ā=Т_А' .

Этот вывод дает возможность находить множество истинности отрицания высказывательной формы по множеству истинности данной высказывательной формы.

Например, дана форма А(х): «х<5», хÎ{1; 2; 3; 4; 5; 6; 7; 8; 9}, ее множество истинности Т_А={1; 2; 3; 4}, тогда множеством истинности Ā(х) будет – Т'_А={5;6;7;8;9}. Мы нашли это множество Т'_А, хотя и не сформулировали саму высказывательную форму Ā(х). Теперь для проверки сформулируем отрицание данной высказывательной формы и найдем ее множество истинности. Отрицанием будем высказывательная форма Ā(х): «Неверно, что х<5» или, что то же самое, Ā(х): «х≥5», ее множество истинности Т_Ā=Т'_А={5;6;7;8;9}.

Теперь выясним, как нужно образовывать отрицание высказываний, содержащих кванторы. Достаточно ли для отрицания таких предложений использовать частицу «не» или слово «неверно»?

Например.

1. Для высказывания: «Всякий прямоугольный треугольник является равнобедренным» будет ли отрицанием высказывание «Всякий прямоугольный треугольник не является равнобедренным»? Очевидно, что не будет, т.к. оба высказывания ложны. Таким образом, строить отрицание высказываний с кванторами при помощи частицы «не» перед сказуемым нельзя.

2. Используем другой путь – перед всем высказыванием поставим слова «неверно, что». Тогда отрицанием высказывания «Всякий прямоугольный треугольник является равнобедренным» является высказывание «Неверно, что всякий прямоугольный треугольник является равнобедренным» или, иначе, высказывание того же смысла «Некоторые прямоугольные треугольники не являются равнобедренными». Как видно, квантор общности меняется на квантор существования и высказывательная форма заменяется отрицанием.

Таким образом, для построения отрицания высказывания с кванторами нужно:

1) квантор общности заменить на квантор существования или, наоборот, квантор существования заменить на квантор общности;

2) для высказывательной формы (предиката) сформулировать отрицание.

В символах это правило можно записать:

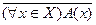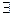= ( х ÎХ) Ā(х);

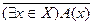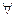= ( х ÎХ) Ā(х).

Если задана словесная формулировка высказывания с кванторами, то нужно: 1) слово «всякий» («каждый», «любой», «все») заменить на слово «существует» («есть», «имеется», «найдется», «некоторый», «хотя бы один») и наоборот; 2) поставить частицу «не» перед сказуемым в высказывательной форме.

Например.

1. Дано высказывание: (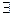xÎZ)(x+5=8), оно истинно. Образуем его отрицание: (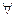xÎZ)(х+5≠8) – это высказывание ложно.

2. Для ложного высказывания (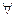xÎR) (х<10) отрицанием будет: (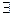xÎR)(х`<10)=(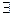хÎR) (х≥10) – это высказывание истинно.

3. Дано высказывание: «Любое дерево есть растение», оно истинно. Его отрицание: «Некоторые деревья не являются растениями» - ложно.

4. Дано высказывание: «Некоторые треугольники являются равнобедренными», оно истинно. Его отрицание: «Любой треугольник является равнобедренным» - ложно.