Высказывания с кванторами. 1. Пусть на множестве N задана высказывательная форма А(х): «Число х кратно 3»

Рассмотрим примеры.

1. Пусть на множестве N задана высказывательная форма А(х): «Число х кратно 3». Поставим перед высказывательной формой слово «всякое». Получим ложное высказывание: «Всякое число х кратно 3» (х ÎN). Поставив перед данной высказывательной формой слово «существует», получим истинное высказывание: «Существует число х, кратное 3» (х Î N).

2. Рассмотрим числа: 1, 2, 3, 4, 5. Про них можно сказать: «Все числа однозначные. Некоторые из данных чисел чётные».

Относительно этих предложений имеет смысл вопрос, истинны они или ложны, следовательно эти предложения – высказывания.

Итак, высказывательную форму (предикат) можно превратить в высказывание, поставив перед формой особые слова, которые называются логике кванторами.

Слово «квантор» произошло от латинского «quantum», что означает «сколько».

Квантором называют символ математической логики, указывающий на определенную логическую операцию, которую необходимо осуществить, чтобы дать количественную характеристику некоторой области объектов.

Таким образом, квантор показывает, о скольких объектах (элементах) говорится в том или ином высказывании.

Различают два основных вида кванторов: квантор общности и квантор существования. Под квантором общности понимаются слова: «любой», «каждый», «всякий», «все», а под квантором существования подразумеваются слова и обороты: «существует», «найдется хотя бы один», «есть», «имеется».

Пусть Р(х) – высказывательная форма (предикат), заданная на множестве Х. Поставив перед ней квантор общности, получим высказывание: «Для всех хÎХ выполняется высказывательная форма Р(х)», которое записывается в символах: ( 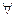xÎX) P(x).

Символ 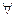– это перевернутая первая буква английского слова «All» - «все».

Высказывание, содержащее квантор общности, истинно в том и только в том случае, если для всех элементов х из множества Х выполняется высказывательная форма Р(х); если же хотя бы для одного элемента х из множества Х высказывательная форма Р(х) не выполняется, то высказывание с квантором общности будет ложно.

Если перед высказывательной формой Р(х), хÎХ, поставить квантор существования, то получим высказывание: «Существует такое хÎХ, что выполняется высказывательная форма Р(х)». В символах оно записывается:

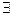( х ÎХ) Р(х).

Символ 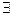- это перевёрнутая справо налево первая буква английского слова «Exist» – «существует».

Высказывание, содержащее квантор существования, истинно в том и только том случае, если хотя бы для одного элемента х из множества Х выполняется высказывательная форма Р(х); если же ни для одного элемента х из множества Х высказывательная форма Р(х) не выполняется, то высказывание с квантором существования ложно.

Например, пусть на множестве N натуральных чисел задана высказывательная форма Р(х): «Число х больше 5». Используя кванторы, из высказывательной формы можно получить, например, следующие высказывания: 1) «Любое натуральное число х больше 5»; 2) «Каждое натуральное число х больше 5»; 3) «Существует натуральное число х, большее 5»; 4) «Найдется натуральное число х, большее 5».

Первые два высказывания имеют одинаковый смысл, они ложны, и в символах запишутся: ( 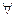xÎN)P(x). Последние два высказывания истинны и имеют запись: ( 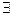xÎN) P(x).

Чтобы установить значение истинности высказываний с кванторами, надо знать некоторые правила.