Эквиваленция высказываний
Рассмотрим составное высказывание, которое образуется из двух элементарных при помощи логической связки «… тогда и только тогда, когда …».
Например, пусть даны высказывания А: «Число 129 делится на 3» и В: «Сумма цифр числа 129 делится на 3». Тогда составное высказывание «Число 129 делится на 3 тогда и только тогда, когда сумма цифр числа 129 делится на 3» имеет структуру «А тогда и только тогда, когда В» и называется эквиваленцией.
Пусть даны высказывания А и В.
Эквиваленцией высказываний А и В называется высказывание, которое истинно, когда оба высказывания А и В истинны или оба ложны одновременно.
Эквиваленция высказываний А и В обозначается: А 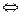 В. Читаем: «Эквиваленция высказываний А и В» или «А тогда и только тогда, когда В» («А в том и только в том случае, если В»).
В. Читаем: «Эквиваленция высказываний А и В» или «А тогда и только тогда, когда В» («А в том и только в том случае, если В»).
Определение эквиваленции высказываний А и В представим в таблице.
| А | В | А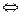 В В
|
| и | и | и |
| и | л | л |
| л | и | л |
| л | л | и |
Примеры.
1. Составное высказывание «Число 18 чётно тогда и только тогда, когда 18M2» истинно, т.к. оба элементарные высказывания «Число 18 чётно» и «18M2» истинны.
2. Составное высказывание «Число 195 делится на 3 тогда и только тогда, когда 195 делится на 9» будет ложным, т.к. оно представляет собой эквиваленцию истинного высказывания «Число 195 делится на 3» и ложного высказывания «Число 195 делится на 9».
3. Составное высказывание «Число 12 простое в том случае, если 12 двузначное число» ложно, т.к. представляет собой эквиваленцию ложного высказывания «Число 12 простое» и истинного высказывания «12 двузначное число».
4. Составное высказывание «12>15 тогда и только тогда, когда 15<12» истинно, т.к. оба составляющие высказывания «12>15» и ложного высказывания «15<12» ложны.
Для эквиваленции высказываний А и В выполняется закон исключения эквиваленции: ( 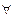 A,B)[A
A,B)[A 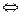 B= (А
B= (А  B)
B) 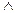 (B
(B  A)].
A)].
Читаем: «Для любых высказываний А и В эквиваленция высказываний А и В равносильна конъюнкции импликации высказываний А и В и импликации высказываний В и А».
Докажем этот закон с помощью таблицы истинности.
| А | В | A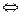 B B
| А B B
| B A A
| (А B) B)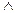 (B (B A) A)
|
| и | и | и | и | и | и |
| и | л | л | л | и | л |
| л | и | л | и | л | л |
| л | л | и | и | и | и |
* *
Сравнивая по сторонам значения истинности для составных высказываний A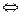 B и (А
B и (А B)
B) 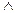 (B
(B A) в столбцах, отмеченных знаком «*», убеждаемся, что эти высказывания равносильны, следовательно, закон исключения эквиваленции доказан.
A) в столбцах, отмеченных знаком «*», убеждаемся, что эти высказывания равносильны, следовательно, закон исключения эквиваленции доказан.
Замечание. В математической логике считают, что: 1) операция конъюнкции «сильнее», чем операции дизъюнкции, импликации и эквиваленции; 2)операция дизъюнкции «сильнее», чем импликация и эквиваленция; 3) операция импликации «сильнее»», чем эквиваленция.
Например, определим порядок действий в составных высказываниях:
а) А B
B 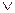 C; б) A
C; б) A 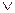 B
B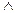 C
C D; в) A
D; в) A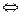 B
B 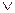 C; г) A
C; г) A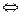 B
B C.
C.
а) Для высказывания А B
B 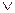 C порядок такой: 1) B
C порядок такой: 1) B 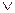 C; 2) А
C; 2) А B
B 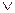 C.
C.
б) Для высказывания A 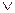 B
B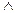 C
C D порядок будет следующий: 1)B
D порядок будет следующий: 1)B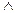 C; 2)A
C; 2)A 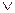 B
B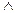 C; 3) A
C; 3) A 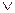 B
B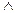 C
C D.
D.
в) В высказывании А B
B 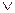 C выполняем: 1) B
C выполняем: 1) B 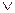 C; 2) А
C; 2) А B
B 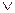 C.
C.
г) В высказывании A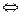 B
B C выполняем: 1) B
C выполняем: 1) B C; 2) A
C; 2) A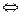 B
B C.
C.
Дата добавления: 2015-10-19; просмотров: 2682;
