Отрицание высказываний. В обыденной речи мы очень часто используем частицу «не» или слова «неверно, что», когда что-нибудь отрицаем
В обыденной речи мы очень часто используем частицу «не» или слова «неверно, что», когда что-нибудь отрицаем. В математике также приходится строить предложения, в которых что-либо отрицается.
Например, говоря, что ∆ АВС является непрямоугольным, мы отрицаем, что ∆ АВС - прямоугольный. При этом, отрицая ложное высказывание, получаем истинное, а отрицая истинное высказывание, получаем ложное.
Пусть дано высказывание А. Определим операцию отрицания высказывания.
Отрицанием высказывания А называется высказывание, которое истинно, когда данное высказывание ложно, и ложно, когда данное высказывание истинно.
Отрицание высказывания А обозначается: Ā. Читаем: «не А» или «неверно, что А».
Например.
1. А: «3+4=7» - это истинное высказывание. Образуем отрицание данного высказывания.
Ā: «3+4≠7» (три плюс четыре не равно 7»), это будет ложное высказывание.
2. В: «7>9» – это ложное высказывание.
`В: «Неверно, что 7>9» или «7 не больше 9». Слова «не больше» означают «меньше или равно», поэтому в символах `Взапишется: «7≤9», это высказывание истинное.
Определение отрицания высказывания можно записать в так называемой таблице истинности.
Таблицей истинности называется таблица, в которой устанавливается значение истинности составного высказывания при различных комбинациях значений истинности входящих в него элементарных высказываний.
Таблица истинности отрицания высказывания имеет вид:
| А | Ā |
| и л | л и |
Пример ознакомления дошкольников с отрицанием «Не А». Наглядный материал изображён на рисунке 15:
яблоко груша апельсин лук
Рис. 15
Задание ребенку: «Выбери лишний предмет, объясни, почему ты так думаешь».
Элементарное предложение: А – «предмет фрукт». Составное предложение: «Не А» – «предмет не является фруктом».
Если предложение А – элементарное высказывание, то для построения отрицания следует либо предварить его словами «неверно, что…», либо поставить частицу «не» перед сказуемым (если А содержит частицу «не», то отбросить ее).
| Выбор ребенка | Значение истинности элементарных предложений А | Оценка воспитателя |
| и | «неправильно» | |
| л | «правильно» |
Для операции отрицания высказывания А выполняется закон, называемый закономдвойного отрицания:
( 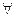 А) (
А) ( 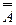 =А).
=А).
Читаем: «Для любого высказывания А двойное отрицание высказывания А равно высказыванию А».
Доказательство этого закона выполняем в следующей таблице истинности, используя определение отрицания высказывания и определение равносильных высказываний.
| А | Ā | 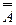
|
| и л | л и | и л |
Как видно из таблицы, значения истинности высказываний А и 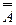 по строкам совпадают, поэтому высказывания А и
по строкам совпадают, поэтому высказывания А и 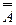 равносильны и равенство А=
равносильны и равенство А= 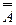 является верным.
является верным.
Убедимся в справедливости этого закона и на примерах.
1. А: «Кызыл – столица Тувы» - и;
Ā: «Кызыл не является столицей Тувы» - л;
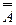 : «Неверно, что Кызыл не является столицей Тувы» - и.
: «Неверно, что Кызыл не является столицей Тувы» - и.
2. В: «2³ = 9» - л;
В: «2³ ≠ 9» - и;
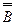 : «Неверно, что 2³ ≠ 9» - л.
: «Неверно, что 2³ ≠ 9» - л.
Дата добавления: 2015-10-19; просмотров: 983;
