Импликация высказываний
Рассмотрим составное высказывание, которое образуется из двух элементарных при помощи логической связки «если …, то …».
Например, пусть даны высказывания А: «Вчера было воскресенье» и В: «Я не был на работе». Тогда составное высказывание «Если вчера было воскресенье, то я не был на работе» имеет структуру «Если А, то В» и называется импликацией.
Пусть даны высказывания А и В.
Импликацией высказываний А и В называется высказывание, которое ложно, когда высказывание А истинно, а высказывание В ложно.
Импликация высказываний А и В обозначается: А  В. Читаем: «Импликация высказываний А и В» или «Если А, то В» (Иногда читают и по-другому: «Из А следует В», «В следует из А»).
В. Читаем: «Импликация высказываний А и В» или «Если А, то В» (Иногда читают и по-другому: «Из А следует В», «В следует из А»).
Высказывание А, входящее в импликацию А В, называют условием импликации, а высказывание В – ее заключением.
В, называют условием импликации, а высказывание В – ее заключением.
Название «импликация» произошло от латинского слова «implico», что значит «тесно связываю».
Определение импликации высказываний А и В дано в следующей таблице истинности.
| А | В | А В В
|
| и | и | и |
| и | л | л |
| л | и | и |
| л | л | и |
Примеры.
1. Составное высказывание «Если число 16 кратно 4, то 16 кратно 2» истинно, т.к. условие импликации «Число 16 кратно 4» истинно и заключение «Число 16 кратно 2» - истинно.
2. Составное высказывание «Если число 16 кратно 4, то 16 кратно 3» ложно, т.к. условие импликации «Число 16 кратно 4» истинно, а заключение «Число 16 кратно 3» - ложно.
3. Составное высказывание «Если число 2∙5=9, то 2>9» истинно, т.к. условие и заключение импликации ложны.
4. Составное высказывание «Если вода в реке соленая, то 2∙2=4» - истинно, т.к. условие импликации «Вода в реке соленая» ложно, а заключение «2∙2=4» - истинно.
Таким образом, из примеров видно, что употребление слов «если …, то …» в логике отличается от употребления их в обыденной речи, где мы, как правило, считаем, что если высказывание А ложно, то высказывание «Если А, то В» вообще не имеет смысла. Кроме того, строя предложения вида «Если А, то В» в обыденной речи, мы почти всегда подразумеваем, что предложение В следует из предложения А, а употребление слов «если …, то …» в логике не требует этого, поскольку, как уже отмечалось ранее, сам смысл высказываний в логике не рассматривается. Поэтому с точки зрения логики и допустимы такие, например, импликации: «Если вода в реке соленая, то 2∙2=4», где условие и заключение по смыслу никаким образом не связаны между собой, но по определению она, как мы выявили выше, истинна.
Операция импликации высказываний А и В может быть выражена через операции отрицания и дизъюнкции, т.е. имеет место следующий закон, называемый законом исключения импликации:
( 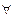 A,B)(A
A,B)(A  B=Ā
B=Ā 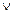 B).
B).
Читаем: «Для любых высказываний А и В импликация высказываний А и В равносильна дизъюнкции отрицания высказывания А и высказывания В».
Равносильность составных высказываний A B и Ā
B и Ā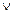 B легко устанавливается при помощи следующей таблицы истинности.
B легко устанавливается при помощи следующей таблицы истинности.
| А | В | A B B
| Ā | Ā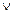 B B
|
| и | и | и | л | и |
| и | л | л | л | л |
| л | и | и | и | и |
| л | л | и | и | и |
* *
Сравнивая в этой таблице по всем строкам значения истинности для составных высказываний A B и Ā
B и Ā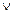 B в столбцах, отмеченных знаком «*», убеждаемся, что все значения совпадают, следовательно высказывания A
B в столбцах, отмеченных знаком «*», убеждаемся, что все значения совпадают, следовательно высказывания A B и Ā
B и Ā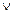 B равносильны, а равенство A
B равносильны, а равенство A B=Ā
B=Ā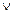 B верно. Таким образом, сказать «Если А, то В» все равно, что сказать «Не А или В».
B верно. Таким образом, сказать «Если А, то В» все равно, что сказать «Не А или В».
Важное значение в дальнейшем будет иметь ещё один закон, называемый законом контрапозиции:
( 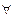 A,B) (A
A,B) (A  B=`B
B=`B  `А).
`А).
Читаем: «Для любых высказываний А и В импликация высказываний А и В равносильна импликации отрицания высказывания В и отрицания высказывания А».
Доказать этот закон также можно при помощи таблицы истинности.
| А | В | A B B
| `В | `А | `B `А `А
|
| и | и | и | л | л | и |
| и | л | л | и | л | л |
| л | и | и | л | и | и |
| л | л | и | и | и | и |
Таким образом, составные высказывания A B и `B
B и `B `А равносильны и равенство A
`А равносильны и равенство A B=`B
B=`B `А верно.
`А верно.
Этот закон позволяет для любой импликации образовывать равносильную ей импликацию.
Например, для импликации «Если сумма цифр числа 111 делится на 3, то число 111 делится на 3» образуем импликацию «Если число 111 не делится на 3, то сумма цифр числа 111 не делится 3», причем обе импликации будут равносильными, т.к. обе они истинны. Первая импликация истинна, т.к. у нее условие и заключение истинны; вторая же импликация истинна, т.к. у нее условие и заключение ложны, а в этом случае по определению импликация тоже истинна.
Для импликации высказываний A B необходимо уметь образовывать отрицание. По закону исключения импликации мы имеем, что A
B необходимо уметь образовывать отрицание. По закону исключения импликации мы имеем, что A B=Ā
B=Ā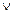 В. Поэтому можно записать:
В. Поэтому можно записать: 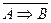 =
= 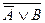 . Используя закон де Моргана для отрицания дизъюнкции, получим:
. Используя закон де Моргана для отрицания дизъюнкции, получим: 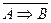 =
= 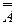
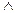 `В=A
`В=A 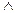 `B, т.к.
`B, т.к. 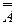 =A по закону двойного отрицания. Значит,
=A по закону двойного отрицания. Значит, 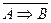 =А
=А 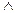 `B.
`B.
Таким образом, отрицание импликации высказываний А и В равносильно конъюнкции высказывания А и отрицания высказывания В.
Дата добавления: 2015-10-19; просмотров: 1857;
