Если несколько простых высказываний объединены в одно с помощью логических операций и скобок, то такое высказывание называется сложным.
Скобки необходимы для определения порядка выполнения логических операций. Примеры сложных высказываний:
| СЛОЖНОЕ ВЫСКАЗЫВАНИЕ | СОСТАВЛЯЮЩИЕ ПРОСТЫЕ ВЫСКАЗЫВАНИЯ | ФОРМА СЛОЖНОГО ВЫСКАЗЫВАНИЯ |
| Е = Идет дождь, а у меня нет зонта | А = Идет дождь; В = У меня есть зонт | 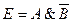
|
| Е = Когда живется весело, то и работа спорится | А = Живется весело; В = Работа спорится | 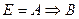
|
| Е = Идет налево – песнь заводит, направо – сказку говорит | А = Идет налево; В = Идет направо; С = Песнь заводит; D = Сказку говорит | 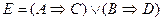
|
В формальной логике принято, что всякое простое высказывание обязательно имеет одно из двух значений – истина или ложь. Следует отметить, что значение не всегда известно. Примерами таких высказываний являются недоказанные или неопровергнутые гипотезы: предположение о существовании жизни на Марсе и т.п. Однако в случае простого высказывания всегда допустимо договориться о том, считать его истинным или ложным.
Сложное высказывание также является истинным или ложным, но это значение вычисляется. Вычисление производится по форме сложного высказывания в соответствии с таблицами истинности входящих в него логических операций. Следовательно, для определения значения истинности сложного высказывания надо уметь определять форму и знать правила логических операций.
Реальную задачу получаем, как правило, в виде текста на естественном языке. И прежде чем приступить к ее решению, надо выделить простые высказывания, отношения (связи) между ними и перевести их на язык формул (формализовать условие задачи, определить форму сложного высказывания).
При вычислении значения логического выражения (формулы) логические операции вычисляются в определенном порядке, согласно их приоритету:
1) инверсия; 2) конъюнкция; 3) дизъюнкция; 4) импликация и эквивалентность.
Операции одного приоритета выполняются слева направо. Для изменения порядка действий используются скобки.
| ДАНА ФОРМУЛА: | ПОРЯДОК ВЫЧИСЛЕНИЙ: | |
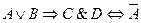
| 1) 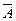
| - инверсия; |
2) 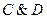
| - конъюнкция; | |
3) 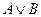
| - дизъюнкция; | |
4) 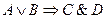
| - импликация; | |
5) 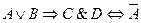
| - эквивалентность. | |
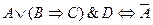
| 1) 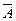
| - инверсия; |
2) 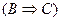
| - импликация в скобках; | |
3) 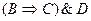
| - конъюнкция; | |
4) 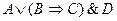
| - дизъюнкция; | |
5) 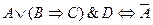
| - эквивалентность. |
Значение сложного высказывания определяется по таблице истинности. Рассмотрим примеры определения значений сложных высказываний.
Дата добавления: 2015-09-11; просмотров: 2760;
