Построим таблицу истинности для высказывания
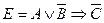 .
.
Алгоритм построения таблицы истинности сложного высказывания (на примере n=3):
1. Вычислить количество строк и столбцов таблицы истинности.
Пусть сложное высказывание состоит из n простых. Тогда количество строк в таблице истинности равно 2n плюс 2 строки заголовка. Количество столбцов в таблице равно сумме количества переменных (n) и количества разных логических операций, входящих в сложное высказывание.
В высказывание Е входят 3 переменные: А, В, С (n=3) и 4 логические операции: инверсия В, инверсия С, дизъюнкция, импликация. Имеем 23 + 2 = 10 строк и 3 + 4 = 7 столбцов.
2. Начертить таблицу и заполнить заголовок.
В первой строке заголовка записываем номера столбцов, во втором – промежуточные формулы в соответствии с приоритетом логических операций и в скобках условные записи операций над значениями пар столбцов, содержащих номера этих столбцов.
3. Заполнить первые 3 столбца.
Количество строк со значениями переменных равно 8.
8:2=4: в 1-м столбце чередуем 4 нуля и 4 единицы.
4:2=2: во 2-м столбце чередуем 2 нуля и 2 единицы.
2:2=1: в 3-м столбце чередуем 1 ноль и 1 единицу.
Таким образом, все возможные комбинации значений переменных учтены и никакие две не совпадают. Фактически такое заполнение столбцов соответствует двоичной записи чисел от 0 до 7.
4. Заполнить остальные столбцы.
Столбцы с 4-го по 7-й заполняем в соответствии с таблицами истинности соответствующих логических операций, причем при заполнении каждого столбца операции выполняются над значениями одного или двух столбцов, расположенных левее заполняемого.
Действуя по этому алгоритму, получим для данного высказывания следующую таблицу:
| А | В | С | 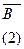
| 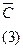
| 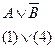
| 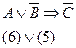
|
Если в формулу входят 4 переменные, то соответствующая ей таблица истинности будет состоять из 24 = 16 строк со значениями; при 5 переменных в таблице имеем 25 = 32 строки со значениями.
Для любого сложного высказывания можно построить таблицу истинности. Это следует из того, что количество входящих в него переменных конечно и каждая из них может принимать всего два значения.
Дата добавления: 2015-09-11; просмотров: 1730;
