Высказывания и логические связки

Многие математические понятия удобно записывать в виде выражений, содержащих некоторые логические символы. Так, символ 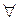, называемый квантором общности, используется вместо слов: «для любого», «для всех», «каково бы ни было…» и т.д., а символ 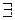– квантор существования – вместо слов «существует», «найдется хотя бы один…», «имеется» и т.д.

Основной объект математической логики - высказывание. Высказыванием называется повествовательное предложение, которое может быть классифицировано либо как истинное, либо как ложное, но не как и то, и другое вместе.

Содержание высказывания несущественно: лишь бы это предложение могло быть либо истинным, либо ложным. При этом вовсе не обязательно указывать способ проверки истинности. Главное, что высказывание не может быть истинным и ложным одновременно. Если высказывание истинно, будем говорить, что его значение истинности - истина (или 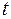(от английского true); если - ложно, то значение истинности – ложь ( 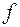от false).

Высказывания в математической логике обычно обозначаются прописными латинскими буквами: , , 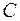и т.д. Для того чтобы из высказываний получать новые высказывания, применяются специальные операции - логические связки. Рассмотрим пять основных логических связок. Сначала дадим неформальное объяснение. Однако оно чревато неточностями, поэтому дадим логическим операциям также строгое определение. Определить высказывание — значит, указать, в каких случаях оно истинно, а в каких ложно.

Отрицание — это высказывание, которое получается из данного высказывания с помощью слова «не». Отрицание можно обозначать по-разному: , , .

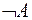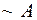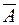Простое добавление слова «не» к высказыванию чаще всего будет противоречить языковым нормам. Поэтому в конкретных случаях требуется «перевод» полученного высказывания на русский язык. Пусть, например, = «Завтра пойдет дождь». Что значит «Не (Завтра пойдет дождь)»: «Дождь пойдет не завтра», «Завтра пойдет не дождь» или «Завтра не пойдет дождь»? Здравый смысл подсказывает, что отрицанием высказывания является третье предложение. Чтобы определить точно, дадим формальное определение отрицания.

Отрицанием 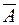высказывания называется такое высказывание, которое принимает значение 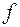(ложно), если высказывание истинно, и значение 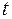(истинно), если высказывание ложно.
В нашем примере этому условию удовлетворяет только третье предложение. Итак, 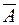= «Завтра не пойдет дождь».

Дизъюнкция - это высказывание, которое получается из двухданных высказываний и с помощью союза «или». Дизъюнкция обозначается .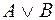

Дизъюнкция строится с помощью неисключающего «или». Таким образом, дизъюнкция 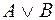истинна, когда истинно, по крайней мере, одно из высказываний и или оба вместе. Другими словами,дизъюнкция ложна в том и только в том случае, когда оба высказывания ложны.

Конъюнкция - это высказывание, которое получается из двух данных высказываний и спомощью союза «и». Конъюнкция обозначается 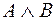. Конъюнкция 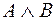справедлива в том и только в том случае, когда оба высказывания истинны.

Импликацияобразуется из высказываний и с помощью слов «если... то...». Получается высказывание вида «если то ». Напомним, что математическая логика носит формальный характер, содержанием высказываний она не, занимается.

На примере импликации хорошо видна разница между обычным языком и языком логики. В обычном языке сложное предложение «если , то » предполагает между и отношение посылки и следствия, или же причины и обусловленного ею действия. В логике импликация связывает любые два высказывания.

Импликация обозначается 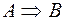, при этом говорят: « влечет » или « при условии, что », « , если », « есть достаточное условие для », « есть необходимое условие для ».

Договорились, что импликация 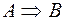ложна в том и только в том случае, когда высказывание истинно, а высказывание ложно. Такое определение подсказано здравым смыслом: разумно считать импликацию истинной, если истинно, независимо от значения ; если оба участника импликации ложны, импликация, естественно, также истинна. В единственном случае, когда «предпосылка» импликации истинна, а «вывод» ложен, импликация считается ложной.

Эквиваленция образуется из высказываний и с помощью слов «...тогда и только тогда, когда...»:

Утверждение « тогда и только тогда, когда » не означает в логике, что составляющие высказывания и имеют одно и то же значение или один и тот же смысл.

Эквиваленция обозначается 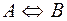. Синонимы для эквиваленции: «если , то , и если , то », « в том и только в том случае, когда », «И есть необходимое и достаточное условие для », « есть необходимое и достаточное условие для ». Разумное определение эквиваленции: эквиваленция истинна в том и только в том случае, когда высказывания и имеют одинаковое значение истинности (либо оба истинны, либо оба ложны).

Новые высказывания (отрицание, дизъюнкция, конъюнкция, импликация и эквиваленция) образуются из существующих высказываний с помощью операций, или логических связок, имеющих те же названия.

В логике, как и в арифметике, операции делятся по старшинству. Это позволяет при записи сложных высказываний избегать большого количества скобок. Порядок выполнения операций таков: приоритет имеет отрицание, затем на одном уровне — дизъюнкция и конъюнкция, следующая связка — импликация и, наконец, самая последняя — эквиваленция.

Контрольные вопросы к лекции №1

1. Понятия доказательного рассуждения и правдоподобного рассуждения.

2. Метод математической индукции.

3. Обобщение, специализация, аналогия.

4. Понятие логической связки.

5. Отрицание, дизъюнкция и конъюнкция.

6. Понятия импликации и эквиваленции.