ЗАКОНЫ ФОРМАЛЬНОЙ ЛОГИКИ
Наиболее простые и необходимые истинные связи между мыслями выражаются в основных законах формальной логики. Таковыми являются законы тождества, непротиворечия, исключенного третьего, достаточного основания.
Эти законы являются основными потому, что в логике они играют особо важную роль, являются наиболее общими. Они позволяют упрощать логические выражения и строить умозаключения и доказательства. Первые три из вышеперечисленных законов были выявлены и сформулированы Аристотелем, а закон достаточного основания – Г. Лейбницем.
Закон тождества: в процессе определенного рассуждения всякое понятие и суждение должны быть тождественны самим себе.
Закон непротиворечия: невозможно, чтобы одно и то же в одно и то же время было и не было присуще одному и тому же в одном и том же отношении. То есть невозможно что-либо одновременно утверждать и отрицать.
Закон исключенного третьего: из двух противоречащих суждений одно истинно, другое ложно, а третьего не дано.
Закон достаточного основания: всякая истинная мысль должна быть достаточно обоснована.
Последний закон говорит о том, что доказательство чего-либо предполагает обоснование именно и только истинных мыслей. Ложные же мысли доказать нельзя. Есть хорошая латинская пословица: «ошибаться свойственно всякому человеку, но настаивать на ошибке свойственно только глупцу». Формулы этого закона нет, так как он имеет только содержательный характер. В качестве аргументов для подтверждения истинной мысли могут быть использованы истинные суждения, фактический материал, статистические данные, законы науки, аксиомы, доказанные теоремы.
Алгебра высказываний (алгебра логики) – раздел математической логики, изучающий логические операции над высказываниями и правила преобразования сложных высказываний. При решении многих логических задач часто приходится упрощать формулы, полученные при формализации их условий. Упрощение формул в алгебре высказываний производится на основе эквивалентных преобразований, опирающихся на основные логические законы.
Законы алгебры высказываний (алгебры логики) – это тавтологии.
Иногда эти законы называются теоремами. В алгебре высказываний логические законы выражаются в виде равенства эквивалентных формул. Среди законов особо выделяются такие, которые содержат одну переменную.
Первые четыре из приведенных ниже законов являются основными законами алгебры высказываний.
Закон тождества: А = А. Всякое понятие и суждение тождественно самому себе.
Закон тождества означает, что в процессе рассуждения нельзя подменять одну мысль другой, одно понятие другим. При нарушении этого закона возможны логические ошибки. Например, рассуждение Правильно говорят, что язык до Киева доведет, а я купил вчера копченый язык, значит, смело могу идти в Киев неверно, так как первое и второе слова «язык» обозначают разные понятия. В рассуждении: Движение вечно. Хождение в школу – движение. Следовательно, хождение в школу вечно слово «движение» используется в двух разных смыслах (первое – в философском смысле – как атрибут материи, второе – в обыденном смысле – как действие по перемещению в пространстве), что приводит к ложному выводу.
Закон непротиворечия: 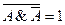 . Не могут быть одновременно истинными суждения и его отрицание. То есть если высказывание А – истинно, то его отрицание не А должно быть ложным (и наоборот). Тогда их произведение будет всегда ложным:
. Не могут быть одновременно истинными суждения и его отрицание. То есть если высказывание А – истинно, то его отрицание не А должно быть ложным (и наоборот). Тогда их произведение будет всегда ложным: 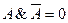 . Именно это равенство используется при упрощении сложных логических выражений.
. Именно это равенство используется при упрощении сложных логических выражений.
Иногда этот закон формулируется так: два противоречащих друг другу высказывания не могут быть одновременно истинными. Пример невыполнения закона непротиворечия: На Марсе есть жизнь и на Марсе нет жизни.
Закон исключенного третьего: 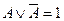 . В один и тот же момент времени высказывание может быть либо неистинным, либо ложным, третьего не дано. Истинно либо А, либо не А.
. В один и тот же момент времени высказывание может быть либо неистинным, либо ложным, третьего не дано. Истинно либо А, либо не А.
Примеры выполнения закона исключенного третьего: Число 12345 либо четное, либо нечетное, третьего не дано. Закон исключенного третьего не является законом, признаваемым всеми логиками в качестве универсального закона логики. Этот закон применяется там, где познание имеет дело с жесткой ситуацией: «либо – либо», «истина – ложь». Там же, где встречается неопределенность (например, в рассуждениях о будущем), закон исключенного третьего часто не может быть применим. Рассмотрим следующее высказывание: Это предложение ложно. Оно не может быть истинным, потому что в нем утверждается, что оно ложно. Но оно не может быть и ложным, потому что тогда оно было бы истинным. Это высказывание не истинно и не ложно, а потому нарушается закон исключенного третьего. Парадокс (неожиданный, странный) в этом примере возникает из-за того, что предложение ссылается само на себя. Другим известным парадоксом является задача о парикмахере: В одном городе парикмахер стрижет волосы всем жителям, кроме тех, кто стрижет себя сам. Кто стрижет волосы парикмахеру? В логике из-за ее формальности нет возможности получить форму такого ссылающегося самого на себя высказывания. Это еще раз подтверждает мысль о том, что с помощью алгебры логики нельзя выразить все возможные мысли и доводы.
Закон двойного отрицания: 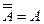 . Если отрицать дважды некоторые высказывания, то в результате получается исходное высказывание.
. Если отрицать дважды некоторые высказывания, то в результате получается исходное высказывание.
Свойства констант:
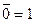 (отрицание лжи есть истина)
(отрицание лжи есть истина)
| 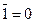 (отрицание истины есть ложь)
(отрицание истины есть ложь)
|
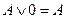
| A&0 = 0 |
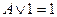
| A&1 = A |
Законы идемпотентности:
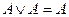 (отсутствие коэффициентов)
(отсутствие коэффициентов)
| 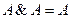 (отсутствие степеней)
(отсутствие степеней)
|
Законы коммутативности:
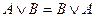
| 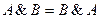
|
Дата добавления: 2015-09-11; просмотров: 1584;
