Высказывания и операции над ними. Повествовательное предложение, о котором можно сказать, истинно оно или ложно, называется высказыванием.
Повествовательное предложение, о котором можно сказать, истинно оно или ложно, называется высказыванием.
Обозначаются высказывания большими буквами латинского алфавита: А, В, С, … X, Y, Z. Высказывания бывают истинными (и) или ложными (л).
Предложение с одной или несколькими переменными, которое преобразуется в высказывание при подстановке вместо всех переменных их значений, называется предикатом.
Примеры:
1. “Студент х изучает психологию” – предикат; “Студент 15 группы изучают психологию” – высказывание.
2. Высказывание А: “Человек – существо мыслящее” – и; высказывание В: “Насекомое – существо мыслящее” – л.
Высказывание, представляющее собой одно утверждение (истинное или ложное), называется элементарным (простым) высказыванием.
Высказывание, образованное из элементарных, называется составным или сложным.
Образование составного высказывания из элементарных называется логической операцией.
Существуют следующие операции над высказываниями: отрицание, конъюнкция, дизъюнкция, импликация и эквиваленция.
Отрицанием высказывания А называется высказывание 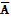 (А) – “не А”, которое является истинным тогда, когда высказывание А ложно, а ложным – тогда, когда А истинно.
(А) – “не А”, которое является истинным тогда, когда высказывание А ложно, а ложным – тогда, когда А истинно.
Набор всевозможных значений истинности для А и 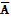 отражает таблица 2.1, называемая таблицей истинности.
отражает таблица 2.1, называемая таблицей истинности.
Таблица 2.1
| A | 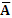
| 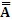
|
| И | Л | И |
| Л | И | Л |
Отрицание любого высказывания можно построить с помощью слов:
“неверно, что”  . Поскольку А – высказывание, то можно построить его отрицание
. Поскольку А – высказывание, то можно построить его отрицание 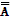 – двойное отрицание. Очевидно, что А=
– двойное отрицание. Очевидно, что А= 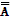 (см. табл. 2.1).
(см. табл. 2.1).
Конъюнкцией двух высказываний А и В называется составное высказывание A 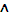 B (А&В) – “А и В”, которое истинно в том, и только в том случае, когда оба высказывания А и В истинны. Набор всевозможных значений истинности конъюнкции показан в таблице 2.2:
B (А&В) – “А и В”, которое истинно в том, и только в том случае, когда оба высказывания А и В истинны. Набор всевозможных значений истинности конъюнкции показан в таблице 2.2:
Таблица 2.2
| A | B | A 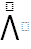 B B
|
| И | И | И |
| И | Л | Л |
| Л | И | Л |
| Л | Л | Л |
Дизъюнкцией двух высказываний А и В называется составное высказывание AvB – “А или В” , которое является истинным тогда, когда хотя бы одно из высказываний А или В истинно. Таблица истинности дизъюнкции – табл. 2.3
Таблица 2.3
| A | B | AvB |
| И | И | И |
| И | Л | И |
| Л | И | И |
| Л | Л | Л |
Импликацией двух высказываний А и В называют составное высказывание А 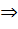 В (А→В) “если А, то В”, которое ложно тогда и только тогда, когда первое высказывание, т.е. А, истинно, а В ложно. Таблица истинности импликации – табл. 2.4
В (А→В) “если А, то В”, которое ложно тогда и только тогда, когда первое высказывание, т.е. А, истинно, а В ложно. Таблица истинности импликации – табл. 2.4
Таблица 2.4
| A | B | A 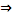 B B
|
| И | И | И |
| И | Л | Л |
| Л | И | И |
| Л | Л | И |
Эквиваленцией двух высказываний А и В называется составное высказывание AóB (А↔В) – “А тогда и только тогда, когда В”, которое является истинным тогда и только тогда, когда оба высказывания одновременно либо истинны, либо ложны. Таблица истинности эквиваленции – табл. 2.5
Таблица 2.5
| A | B | A⇔B |
| И | И | И |
| И | Л | Л |
| Л | И | Л |
| Л | Л | И |
Следует сделать оговорку, что логические операции не учитывают смысл высказываний; они рассматриваются как объекты, обладающие единственным свойством – быть истинными и ложными.
Примеры:
1. Высказывание А: “Брестский государственный университет им. А.С. Пушкина был основан в 1945 году”; высказывание 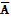 : “Неверно, что Брестский государственный университет им. А.С. Пушкина был основан в 1945 году ”.
: “Неверно, что Брестский государственный университет им. А.С. Пушкина был основан в 1945 году ”.
2. Высказывание В: “Треугольник АВС прямоугольный”; высказывание : “Неверно, что треугольник АВС прмоугольный”, т.е. “Треугольник АВС – тупоугольный или остроугольный”.
3. Высказывание А: “Студент добросовестно готовился к экзамену”, высказывание В: “Студент сдал экзамен блестяще”, высказывание A  B: “Студент добросовестно готовился к экзамену и сдал его блестяще”.
B: “Студент добросовестно готовился к экзамену и сдал его блестяще”.
4. A  B: «Число 30 двузначное и четное ”.
B: «Число 30 двузначное и четное ”.
5. Высказывание А: “Фестиваль “Славянский базар” проводится в Витебске”, высказывание В: “Брест – самый западный город Беларуси”, Высказывание A  B: “ Славянский базар” проводится в Витебске или Брест – самый западный город Беларуси”.
B: “ Славянский базар” проводится в Витебске или Брест – самый западный город Беларуси”.
6. A  B: “13≤23”.
B: “13≤23”.
7. А 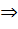 B: “Если число 30 двузначное, то оно четное ”.
B: “Если число 30 двузначное, то оно четное ”.
8. Высказывание А: “Треугольник АВС является прямоугольным”, высказывание В: “Квадрат одной стороны треугольника равен сумме квадратов двух других его сторон”, высказывание AóB: “Треугольник АВС является прямоугольным тогда и только тогда, когда квадрат одной стороны треугольника равен сумме квадратов двух других его сторон”.
9. AóB: “Стать хорошим психологом можно тогда и только тогда, когда овладеешь математическими методами”.
Дата добавления: 2015-09-28; просмотров: 3408;
