Соответствия и отношения

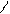Соответствием R между множествами X и Y называется подмножество R декартова произведения Х?Y : R Х?Y.

Множество Х называют областью отправления данного соответствия, а множество У – его областью прибытия.

Если а 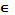Х, то образом этого элемента называется множество R(а) всех элементов у 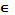У, таких, что аRу. Прообразом элемента в 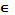У при том же соответствии назовем множество R^-1(в) элементов х Х, таких, что хRв. Образ всего множества Х называется множеством (областью) значений – R(Х), это множество концов всех стрелок. Прообраз всего множества У при соответствии R называют областью определения этого соответствия и обозначают R^-1(У), это множество начал всех стрелок.

Пример:

Возьмем множество учеников Х={Ваня, Даша, Ира} и множество типов темперамента У={сангвиник, холерик, флегматик, меланхолик}. Построим граф соответствия R: «Ученик х обладает темпераментом у».

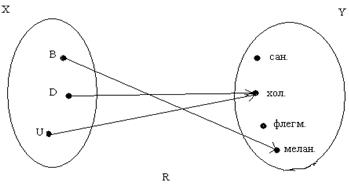
Рис. 1.14

На рис. 1.14: R(Ваня)= {меланхолик}, R(Даша)= {холерик}, R(Ира)={холерик}, R^-1 (сангвиник)= ?, R^-1(флегматик)= ?, R^-1 (холерик)= {Даша, Ира}, R^-1(меланхолик) = {Ваня}. Область определения соответствия R^-1(У)= =Х={Ваня, Даша, Ира}, множество значений R(Х)= {холерик, меланхолик}.

_____________________________________________________________

Если при соответствии R образ каждого элемента х Х или пуст, или содержит лишь один элемент, то R называют функциональным соответствием или функцией. Другими словами, соответствие R функционально, если из того, что хRу₁ и хRу₂, можно сделать вывод, что у₁=у₂.

Соответствие R, для которого области отправления и прибытия совпадают, называется отношением, заданным на множестве Х. Для элементов х и у из множества Х, связанных отношением R, можно записать: хRу или R(х)=у.

Отношение R, заданное на множестве Х, называется рефлексивным, если для всех х Х выполняется хRх.

Отношение R, заданное на множестве Х, называется антирефлексивным, если ни для какого х 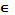Х не выполняется хRх.

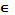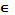Отношение R, заданное на множестве Х, называется симметричным, если для всех х Х, у Х выполняется: если хRу, то уRх.

Отношение R, заданное на множестве Х, называется асимметричным, если ни для каких х 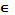Х, у 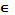Х не выполняется: если хRу, то уRх.

Отношение R, заданное на множестве Х, называется антисимметричным, если для х 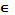Х, у 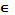Х выполняется: если хRу и уRх, то х=у.

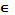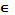Отношение R, заданное на множестве Х, называется транзитивным, если для х Х, у Х, z 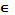Х, выполняется: если хRу и уRz, то хRz.

Пример:

Рассмотрим отношение R: «учиться в одной группе» на множестве студентов. Проверим выполнение следующих свойств:

1. Рефлексивность: для любого студента х выполняется хRх, т.е. «студент х учится в одной группе сам с собой» - и.

2. Симметричность: для двух студентов х и у выполняется если хRу, то уRх, т.е. «если студент х учится в одной группе со студентом у, то студент у учится в одной группе со студентом х» - и.

3. Транзитивность: для трех студентов х, у, z выполняется: если хRу и уRz, то хRz, т.е. «если студент х учится в одной группе со студентом у, а студент у учится в одной группе со студентом z, то студенты х и z учатся в одной группе» - и.

Отношение R на множестве Х называется отношением эквивалентности, если оно рефлексивно, симметрично, транзитивно. Рассмотренное в примере отношение «учиться в одной группе»на множестве студентов является отношением эквивалентности.

Отношение R на множестве Х называется отношением толерантности, если оно рефлексивно и симметрично. Примером отношения толерантности может служить отношение «быть знакомым» на множестве людей.

Отношение R на множестве Х называется отношением строгого порядка, если оно антирефлексивно, асимметрично, транзитивно. Примерами являются отношения «выше», «дальше», «тяжелее».

Отношение R на множестве Х называется отношением нестрогого порядка, если оно рефлексивно, антисимметрично, транзитивно. Примерами являются отношения «не выше», «не меньше», «не больше».

Рассмотренные отношения и их свойства находят применение при составлении тестов, в вопросах голосования и т.д.