ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
Матрицы. Основные понятия
Матрицей размера т?п называется прямоугольная таблица чисел, содержащая т строк и п столбцов.
Элементами матрицы называются числа, составляющие матрицу.
Матрицы обозначаются прописными (заглавными) буквами латинского алфавита, например, А, В, С,.. или иначе А = (а), В=(b)…. Для обозначения элементов матрицы используются строчные буквы с двойной индексацией: аij, где i — номер строки, j — номер столбца. Матрица размера т?п имеет вид:
А= 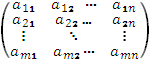
Равными называются матрицы А = (а)и В=(b) одинакового размера, если они совпадают поэлементно, т.е. аij =bij для любых i = 1,2,..., т; j = 1,2,..., п.
Примеры:
_______________________________________________________________________________
1) Для матрицы A = 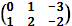
элементами являются: а11 = 0, а12 = 1, а13 = -3, a21 = 1, а22 = 2, а23 = -2.
2) Для матриц С и В
C = 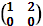 , B =
, B = 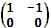
С 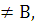 так как элементы а12 = 2и b12 =-1 не совпадают.
так как элементы а12 = 2и b12 =-1 не совпадают.
-------------------------------------------------------------------------------------------------___________________________
Матрицей-строкой называется матрица, состоящая из одной строки.
Матрицей-столбцом называется матрица, состоящая из одного столбца.
Квадратной матрицей порядка п называется матрица, у которой число строк равно числу столбцов и равно п .
 Диагональной называется матрица, у которой все недиагональные элементы равны 0.
Диагональной называется матрица, у которой все недиагональные элементы равны 0.
Главную диагональ квадратной матрицы порядка п образуют элементы a11, a22 , ... , ann.
A = 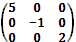 – диагональная матрица третьего порядка.
– диагональная матрица третьего порядка.
Единичной называется диагональная матрица, у которой все диагональные элементы равны 1, остальные нули. Например,
E = 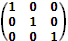 – единичная матрица третьего порядка.
– единичная матрица третьего порядка. 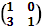
 E.
E.
Дата добавления: 2015-09-28; просмотров: 573;
