Формулы и законы логики высказываний
Логической формулой, или формулой логики высказываний называется предложение, составленное из элементарных (простых) высказываний (А, В, С, … X, Y, Z), знаков логических операций (,  ,
,  ,
, 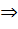 , ó) и скобок.
, ó) и скобок.
Для того, чтобы из из высказывания получить формулу, надо:
1) выделить все элементарные высказывания и логические операции, образующие данное составное высказывание;
2) заменить их соответствующими буквами и символами;
3) расставить скобки в соответствии со смыслом данного высказывания.
Пример:
Дано предложение: “Если человек доброжелателен и контактен, то с ним легко общаться”. Обозначим: А – “Человек является доброжелательным”, В – “Человек является контактным”, С – “С человеком легко общаться”. Формула будет такой: (A  B)
B) 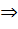 С
С
Логические операции выполняются в следующей последовательности: ,  ,
,  ,
, 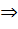 , ó. Это позволяет упрощать запись, избавляясь от лишних скобок. Например, вместо формулы
, ó. Это позволяет упрощать запись, избавляясь от лишних скобок. Например, вместо формулы
((A  B)
B)  (
( 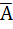
 В))
В)) 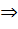 (
(  ) можно записать A
) можно записать A  B
B 
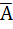
 В
В 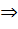
 .
.
Способ “вычисления истинности” логических формул – построение таблицы истинности.
Пример:
Построить таблицу истинности для формулы 
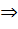 В.
В.
Таблица 2.6
| А | В | 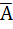
| 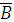
| 
|  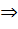 В В
|
| и | и | л | л | л | и |
| и | л | л | и | и | л |
| л | и | и | л | и | и |
| л | л | и | и | и | л |
Если формула содержит три переменных, то для нее будет 8 различных наборов значений истинности. Если в формуле п переменных, то различных наборов значений истинности будет 2п..
Две логические формулы называются равносильными, если их таблицы истинности совпадают.
В логике высказываний существуют следующие равносильности или законы логики, связанные с законами мышления:
I. А 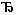 А – закон тождества.
А – закон тождества.
II. A 
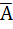
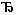 Л – закон противорчия
Л – закон противорчия
III. A 
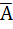
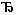 И – закон исключенного третьего
И – закон исключенного третьего
IV. А 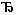
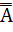 – снятие отрицания
– снятие отрицания
V. A  А
А 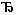 А; A
А; A  А
А 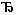 А
А
VI. A  В
В 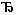 В
В  А; A
А; A  В
В 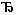 В
В  А – коммутативность
А – коммутативность
VII. (A  В)
В)  С= А
С= А  (В
(В  С); (A
С); (A  В)
В)  С= А
С= А  (В
(В  С) – ассоциативность
С) – ассоциативность
VIII. А  (B
(B  C)
C) 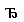 (A
(A  B)
B)  (A
(A  C);A
C);A  (B
(B  C)
C) 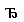 (A
(A  B)
B)  (A
(A  C)–дистрибутивность
C)–дистрибутивность
IX. 
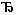
 ;
; 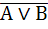
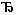
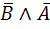 – законы Де Моргана
– законы Де Моргана
X. A  И
И 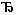 А; A
А; A  Л
Л 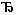 А
А
XI. A  Л
Л 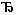 Л; A
Л; A  И
И 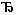 И
И
XII. А  (A
(A  В)
В) 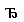 А; A
А; A  (A
(A  В)
В) 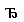 А
А
XIII. (A  В)
В)  (
( 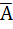
 В)
В) 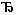 В; (A
В; (A  В)
В)  (
( 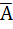
 В)
В) 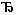 В
В
XIV. А 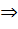 B
B 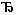
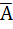
 В; А
В; А 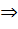 B
B 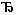
 – замена импликации
– замена импликации
Доказать эти законы можно с помощью таблиц истинности.
Логическая формула называется тождественно истинной или тавтологией, если она принимает только значение “и” при любом наборе значений истинности входящих в нее переменных.
Логическая формула называется тождественно ложной, или противоречием, если она принимает только значение “л” при любом наборе значений истинности входящих в нее переменных.
Тождественно истинные и тождественно ложные формулы играют важную роль в математической логике, так как являются моделями для многих задач. Так, тождественно истинные формулы используются при построении логических выводов одних утверждений из других, тождественно ложные – при анализе совместности утверждений. Аксиомы, теоремы, статьи законодательства – примеры тождественно истинных высказываний.
Логика является незаменимой в психологических иследованиях, где проводится оценка выдвигаемых гипотез (предположений) на предмет их истинности или ложности, которая осуществляется на основе статистических критериев.
Дата добавления: 2015-09-28; просмотров: 1148;
