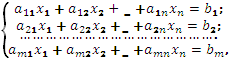Определители квадратных матриц и их свойства
Для каждой квадратной матрицы А вводится число 
, называемое ее
определителем.
Для матрицы первого порядка определитель 
равен ее элементу а11.
Для матрицы второго порядка A =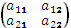 
ее определитель вычисляется следующим образом:
|
(3.1)
 | |
Пример:
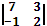= 7⋅2 - 3⋅(-1) = 14 + 3 = 17.
Для матрицы третьего порядка A =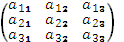 
определитель вычисляется по формуле:
 |
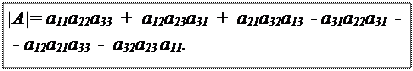() (3.2)
Знаки, с которыми слагаемые входят в формулу (3.2), легко запомнить, пользуясь схемой (рис. 3.1), которая называется правилом треугольника или правилом Саррюса (для знака «плюс» основания равнобедренных треугольников параллельны главной диагонали, для знака «минус» — параллельны побочной диагонали).
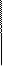а11 а12 а13
+ а 21 а22 а23 –
а31 а32 а33
|
Рис. 3.1
Пример:
Для матрицы A =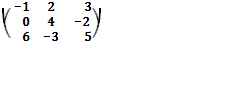 
найдём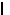 
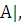пользуясь правилом Саррюса:
|А| = (-1) · 4 · 5 + 2 · (-2) · 6 + 0 · (-3) · 3 – 6· 4 · 3 – 0 · 2 · 5 – (-3) · (-2)· (-1) =
= -20 –24+ 0 – 72– 0+6 = -110.
_______________________________________________________
Свойства определителей:
1. Если какая-либо строка (столбец) матрицы состоит из
одних нулей, то ее определитель равен нулю.
2. Если все элементы какой-либо строки (столбца) матрицы умножить на число, то ее определитель умножится на это число.
3. При перестановке двух строк (столбцов) матрицы ее определитель меняет знак на противоположный.
4. Если матрица содержит две одинаковые строки (столбца), то ее определитель равен нулю.
5. Если элементы двух строк (столбцов) матрицы пропорциональны, то ее определитель равен нулю.
6. Определитель матрицы не изменится, если к элемен-
там какой-либо строки (столбца) прибавить элементы
другой строки (столбца), умноженные на одно и то же
число.
7. 
Определитель произведения двух квадратных матриц
равен произведению их определителей: |C|= |А|·|В|, где
С = А·В.
Системы линейных уравнений. Основные понятия и определения
Системой линейных уравнений с п неизвестными х1,... хп называется
система
|
(3.3)
 |
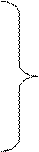где aij, (i =1,2,… m; j =1,2,… n) — произвольные числа, называемые коэффициентами при неизвестных, bi , (i =1,2,… m) – свободными членами уравнений.
Решением системы (3.3) называется такая совокупность п чисел (x1, х2,… xn), что при подстановке их в систему каждое уравнение системы обращается в тождество.
Совместной называется система уравнений, имеющая хотя бы одно решение.
Несовместной называется система уравнений, не имеющая решений.
Определенной называется совместная система уравнений, имеющая единственное решение.
Неопределенной называется совместная система уравнений, имеющая более одного решения.
Пример:
_______________________________________________________________________________
Система уравнений
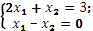
совместная и определенная, так как имеет единственное решение (1,1);
система
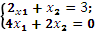
несовместная; а система уравнений
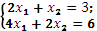
множество решений (х1 = с, x2 = 3 – 2с, где с — любое число).
-------------------------------------------------------------------------------------------------
Равносильными или эквивалентными называются системы уравнений, имеющие одно и то же множество решений.
Элементарными преобразованиями системы (3.3) называются:
1) умножение уравнения системы на число λ≠0;
2) умножение уравнения системы на любое число λ и прибавление полученного произведения к другому уравнению системы;
3) вычеркивание нулевого уравнения (0x1 +0x2 + … +0xn = 0) из системы;
4) перестановка двух уравнений системы.
Справедлива следующая теорема:
Элементарные преобразования системы уравнений преобразуют систему в ей эквивалентную.
Дата добавления: 2015-09-28; просмотров: 775;