Метод Гаусса. Метод Гаусса заключается в том, что элементарные преобразования совершают не над уравнениями системы (3.3)
Метод Гаусса заключается в том, что элементарные преобразования совершают не над уравнениями системы (3.3), а над матрицами, составленными из коэффициентов при неизвестных и свободных членов. Для системы (3.3) запишем расширенную матрицу, последний столбец которой состоит из свободных членов:

С помощью элементарных преобразований строк приведем расширенную матрицу к такому виду, чтобы в последней строке матрицы все члены, кроме п-го, были равны нулю. Система линейных уравнений, соответствующая этой матрице, будет эквивалентна исходной. Затем из последнего уравнения системы, соответствующей преобразованной матрице, находим хп. Все остальные решения могут быть найдены последовательно, начиная с последнего уравнения.
Проиллюстрируем метод Гаусса на примерах с различными видами систем.
Примеры:
__________________________________________________________________________________
1) Решить систему уравнений:

Составим матрицу из коэффициентов при неизвестных и свободных членов (вертикальной чертой отделён столбец из свободных членов). Затем преобразуем её, умножив первую строку поочерёдно на (-1), (-4), (-2) и прибавив соответственно ко второй, третьей, четвёртой строкам. В результате получим из первоначальной матрицы преобразованную:

Второй матрице соответствует система уравнений
Решая последовательно все уравнения системы, начиная с последнего, получим:
 , 20
, 20 
20 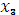 =8 – 3, 20
=8 – 3, 20 

2  =8
=8  +3
+3 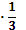 – 4, 2
– 4, 2 

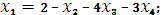
 – 4·
– 4· 
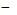 3·
3·  ,
,  .
.
Ответ: 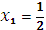 ,
, 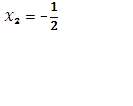 ,
, 
2) Решить систему уравнений


Первую строку матрицы последовательно умножили на (-2), (-5), (-3) и сложили соответственно со второй, третьей и четвертой строками. На втором шаге из третьей строки вычли вторую. В результате получаем, что
система несовместна, т.к. уравнение, соответствующее третьей строке матрицы:
0 
не имеет решения.
3) Решить систему уравнений



 ;
;
;




 ,
,
где х4 – свободное неизвестное, оно может принимать любые действительные значения, т.е. система имеет бесконечное множество решений.
-------------------------------------------------------------------------------------------------
Дата добавления: 2015-09-28; просмотров: 647;
